Is the sparse Hessian mechanism for FindMinimum[] (Method->"Newton") broken? Or am I simply not apprehending its proper setup? Here's what's happening.
Below is for solving the example problem given in
tutorial/UnconstrainedOptimizationNewtonsMethodMinimum#509267359
using specified Gradient g and (dense) Hessian h functions.
The only difference here from the documentation example is I specify g and h as bare symbolic expressions using RuleDelayed rather than as functions with x_?NumberQ type arguments. Nonetheless, the correct result is obtained:
Clear[f, g, h, x, y]
f = Cos[x^2 - 3 y] + Sin[x^2 + y^2]
g = D[f, {{x, y}}]
(* Out[3]= {2 x Cos[x^2 + y^2] - 2 x Sin[x^2 - 3 y], 2 y Cos[x^2 + y^2] + 3 Sin[x^2 - 3 y]} *)
h = D[f, {{x, y}, 2}]
(* Out[4]= {{-4 x^2 Cos[x^2 - 3 y] + 2 Cos[x^2 + y^2] -
2 Sin[x^2 - 3 y] - 4 x^2 Sin[x^2 + y^2],
6 x Cos[x^2 - 3 y] - 4 x y Sin[x^2 + y^2]},
{6 x Cos[x^2 - 3 y] - 4 x y Sin[x^2 + y^2],
-9 Cos[x^2 - 3 y] + 2 Cos[x^2 + y^2] - 4 y^2 Sin[x^2 + y^2]}} *)
FindMinimum[f, {{x, 1}, {y, 1}}, Method -> {"Newton",
"Hessian" :> {h, "EvaluationMonitor" :> Print[h]}},
Gradient :> {g, "EvaluationMonitor" :> Print[g]}]
(* Output:
{0.986301,-3.56019}
{{-0.986301,-6.13407},{-6.13407,-0.724162}}
{-0.527482,2.63714}
{{12.3165,2.2687},{2.2687,20.8245}}
{0.230844,-0.059627}
{{15.6441,0.981772},{0.981772,20.2644}}
{0.00357296,0.0000289779}
{{15.1633,0.983822},{0.983822,20.2729}}
{9.20305*10^-7,7.95904*10^-9}
{{15.1555,0.983708},{0.983708,20.2718}}
{5.85103*10^-14,2.82458*10^-15}
{{15.1555,0.983708},{0.983708,20.2718}}}
Out[5]= {-2., {x -> 1.37638, y -> 1.67868}} *)
Now onto replicating the above, but this time specifying a sparse Hessian. I attempt to follow the setup discussed in:
tutorial/UnconstrainedOptimizationSpecifyingDerivatives#562305099
We first obtain the sparse Hessian function (sparhess), per the cells below:
1. convert the dense 2D list-based Hessian into a SparseArray form,
2. perform the indepotent Transpose[Transpose to force consistent lexicographic array index ordering of the non-zero element Rules
3. obtain those ArrayRules to form our sparse Hessian function, which is a same-ordered 1D list of the non-zero element functions...
4. ... parsing out the RHS expression of each Rule, and omitting the last ArrayRule, which is the default value for "zero" elements:
sphess = SparseArray[h];
sparsity = Transpose[Transpose[sphess]];
arhess = ArrayRules[sparsity]
(* Out[8]={{1, 1} -> -4 x^2 Cos[x^2 - 3 y] + 2 Cos[x^2 + y^2] -
2 Sin[x^2 - 3 y] - 4 x^2 Sin[x^2 + y^2],
{1, 2} -> 6 x Cos[x^2 - 3 y] - 4 x y Sin[x^2 + y^2],
{2, 1} -> 6 x Cos[x^2 - 3 y] - 4 x y Sin[x^2 + y^2],
{2, 2} -> -9 Cos[x^2 - 3 y] + 2 Cos[x^2 + y^2] - 4 y^2 Sin[x^2 + y^2],
{_, _} -> 0} *)
sparhess = arhess[[1 ;; -2, 2]]
(* Out[9]= {-4 x^2 Cos[x^2 - 3 y] + 2 Cos[x^2 + y^2] -
2 Sin[x^2 - 3 y] - 4 x^2 Sin[x^2 + y^2],
6 x Cos[x^2 - 3 y] - 4 x y Sin[x^2 + y^2],
6 x Cos[x^2 - 3 y] - 4 x y Sin[x^2 + y^2],
-9 Cos[x^2 - 3 y] + 2 Cos[x^2 + y^2] - 4 y^2 Sin[x^2 + y^2]}
Next, we obtain the "SparseArray template" (sparsity) which specifies the sparsity pattern (non-zero elements) of the Hessian, per the cells below:
1. Take our earlier ArrayRules (arhess) and replace the RHS of Rules with Pattern "_", omitting the last ArrayRule, which is the default value for "zero" elements
2. Form a SparseArray from these ArrayRules
3. To be safe, do the trick to force consistent internal ArrayRule ordering:
arhess = Map[ReplacePart[#, 2 -> _] &, arhess[[1 ;; -2]]]
(* Out[10]= {{1, 1} -> _, {1, 2} -> _, {2, 1} -> _, {2, 2} -> _} *)
sparsity = SparseArray[arhess];
sparsity = Transpose[Transpose[sparsity]];
Now finally onto employing this in FindMinimum:
FindMinimum[f, {{x, 1}, {y, 1}}, Method -> {"Newton",
"Hessian" :> {sparhess, "Sparse" -> sparsity,
"EvaluationMonitor" :> Print[sparhess]}},
Gradient :> {g, "EvaluationMonitor" :> Print[g]}]
(* Output:
{0.986301,-3.56019}
{-0.986301,-6.13407,-6.13407,-0.724162}
{-9.46857,-4.5823}
{-13.6137,-3.30307}
{0.0908205,0.636614}
{1.36673,-0.619934,-0.619934,6.60192}
{-0.111213,-0.102242}
{2.29398,0.384308,0.384308,7.15042}
{-0.00442004,-0.00834982}
{2.19695,0.0162966,0.0162966,7.16648}
{-0.0000188381,-0.0000167613}
{2.18754,0.000069903,0.000069903,7.16556}
{-1.63506*10^-10,-3.03399*10^-10}
{2.18752,6.06735*10^-10,6.06735*10^-10,7.16555}
Out[13]= {-0.179902, {x -> -7.47451*10^-11, y -> 0.905726}} *)
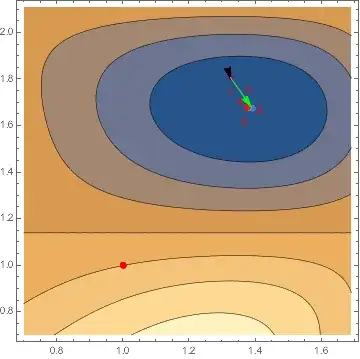
Wrong Answer! Comparing the gradient and hessian values printout for this FindMinimum run to the earlier correct run, we see that the first gradient and Hessian values are identical, but then our sparse version goes off the rails.
Interestingly, rerunning the above as so, using our original dense Hessian h to drive the minimization, setting "Sparse" to False, but along the minimization path printing out the values of sparhess, we observe the correct values being computed from sparhess (!?):
FindMinimum[f, {{x, 1}, {y, 1}}, Method -> {"Newton",
"Hessian" :> {h, "Sparse" -> False,
"EvaluationMonitor" :> Print[sparhess]}},
Gradient :> {g, "EvaluationMonitor" :> Print[g]}]
(* Output:
{0.986301,-3.56019}
{-0.986301,-6.13407,-6.13407,-0.724162}
{-0.527482,2.63714}
{12.3165,2.2687,2.2687,20.8245}
{0.230844,-0.059627}
{15.6441,0.981772,0.981772,20.2644}
{0.00357296,0.0000289779}
{15.1633,0.983822,0.983822,20.2729}
{9.20305*10^-7,7.95904*10^-9}
{15.1555,0.983708,0.983708,20.2718}
{5.85103*10^-14,2.82458*10^-15}
{15.1555,0.983708,0.983708,20.2718}
Out[14]= {-2., {x -> 1.37638, y -> 1.67868}} *)




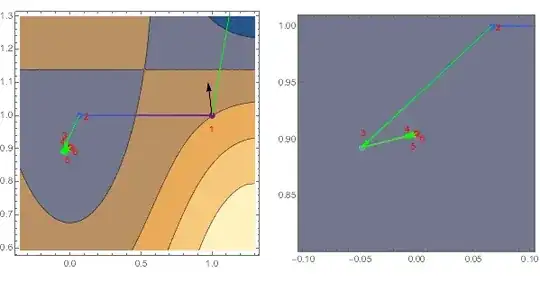
SparseArray[]? Or, is this a toy example, and something similar happens to your actual application? – J. M.'s missing motivation Aug 14 '15 at 15:53SparseArrayapproach seems to take a funny first step that lands in a different basin than the default. I haven't been able to figure why the initial step is off. (Monitor withEvaluationMonitor :> Print[eval[x, y, f]], StepMonitor :> Print[step[x, y, f]], ifevalandstepare undefined.) – Michael E2 Aug 15 '15 at 03:56FindMinimummight not take a slightly different approach with the sparse array method. I don't know how the method works, but there may be general issues with a sparse system. For instance, at the initial point{1., 1.}in the simple example, the Hessian is not positive definite, which it should be near a minimum. In sparse systems, it might in general be good to search for better starting point. – Michael E2 Aug 15 '15 at 15:45