Scatter plot with smooth lines

Question

I have two lists of data between which there may be some functional dependence. I want to plot one against the other (hence scattered plot) where the points are connected by smooth lines.

In Microsoft Excel this is done by selecting the two sets of data and then selecting "scattered with smooth line" option. How can i do that same thing in Mathematica?

Hi, welcome to Mathematica.SE, please consider taking the tour so you learn the basics of the site. Once you gain enough reputation by making good questions you will be able to vote up and down both questions and answers. When you see good ones, please vote them up by clicking the grey triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. As you receive help, try to give it too, by answering questions in your area of expertise. — rhermans, Aug 19 '15 at 16:51
you might want to give ListLinePlot the option InterpolationOrder -> 3 to mimic excel's "smooth line". (personally I would never use that for "data" ) — george2079, Aug 19 '15 at 16:51
Your question may be put on-hold because it could be considered off-topic as the answer is trivially found in the documentation. Please don't be discouraged by that cleaning-up policy. Your questions are and will be most welcomed. Learn about good questions here. — rhermans, Aug 19 '15 at 16:52
Thanks. I've become so habituated to ask question and get help from stackexchange that i've forget to search documentation. What a lethargic person the internet has made me! — Sabbir Ahmed, Aug 19 '15 at 16:58

score 10 · Accepted Answer · edited Apr 13 '17 at 12:55

10

I think you might be after a "smoothed" presentation such as the following:

SeedRandom[35]
data = Table[{x, x^2 + RandomReal[20]}, {x, -10, 10, 1}];
ListPlot[{data, data}, Joined -> {False, True}, InterpolationOrder -> 3]

cubic spline interpolation

However, I would caution you against using this kind of interpolated presentation unless you are very sure that it is appropriate in your case. I would typically consider it bad practice to join experimental data with interpolation lines unless those lines have a physical meaning.

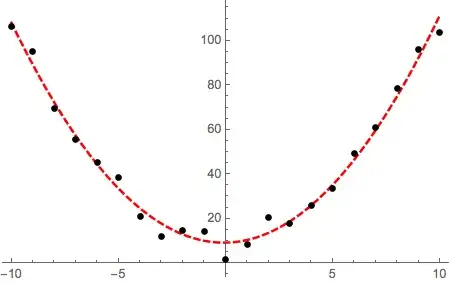
It would be more informative instead if you attempted to fit the data to the functional expression that represents the assumed functional dependence. For instance, suppose that in this case I suspect that there is quadratic dependence in the data. I can use FindFit or LinearModelFit / NonlinearModelFit (depending on the functional form of your model, see here as well) to find the best-fit parameters, the plot the fit as a continuous line together with a scatter plot of the data points:

nlm = NonlinearModelFit[data, a x^2 + b x + c, {a, b, c}, x];

Plot[
 nlm[x],
 Evaluate@Flatten@{x, Through[{Min, Max}[ data[[All, 1]] ]]},
 PlotStyle -> {Red, Thick, Dashed},
 Epilog -> {PointSize[0.015], Point[data]}
]

fit

edited Apr 13 '17 at 12:55

Community

1

answered Aug 19 '15 at 16:56

MarcoB

67,153
18
91
189

Please see my extended comment disguised as an answer for what I believe is a small improvement to this answer. – m_goldberg Aug 19 '15 at 18:13
Your point is well made: I always hated how Excel produces curves with spurious extrema in between the points. But, sometimes one needs to connect the points in a series somehow for visual clarity, even with no a priori known functional form. (Imagine we have several series in the same plot, which without any lines will tend to become a mess of scattered points.) I prefer using either straight lines joining the points (to make it obvious it is not physical), or a smooth, "freehand" curve that closely follows the points without necessarily joining them (often seen in older papers). – Oleksandr R. Aug 20 '15 at 01:39
@OleksandrR. I think you have a valid point about the need to "group together" data sets in busy plots for readability. Because of that fact, I try to keep the number of data sets to present on one plot to a minimum, when possible. I am curious about the "smooth, freehand curve" you mention though: I don't think I am familiar with that. Could you point me to an example? – MarcoB Aug 20 '15 at 19:00
Like this, for example. The curves are neither fits nor interpolations, but merely pick out the series and suggest a trend. One could get this sort of curve by low-order Savitzky-Golay filtering, or something similar, perhaps. Maybe worth a question in its own right? – Oleksandr R. Aug 21 '15 at 02:01
@OleksandrR. I see now. Thank you. Yes, I think it would be interesting to investigate your point further! – MarcoB Aug 21 '15 at 22:33

m_goldberg · Answer 2 · 2015-08-20T00:00:42.980

4

This is not an answer, but a extended comment on MarcoB's answer, which I think is a good one. However, I would like to suggest an improvement to the way he plots the fit function together with the data, which makes the plot expression independent of the global variable data.

I am assuming that nlm has been defined precisely as shown in MarcoB's answer.

With[{pts = nlm["Data"]},
  Plot[nlm[x],
    Evaluate @ Prepend[MinMax[pts[[All, 1]]], x], 
    PlotStyle -> {Red, Thick, Dashed}, 
    Epilog -> {PointSize[0.015], Point[pts]}]]

plot

edited Aug 20 '15 at 00:00

answered Aug 19 '15 at 18:09

m_goldberg

107,779
16
103
257

Excellent points both, using With, and MinMax. I was actually not aware of MinMax: it will come in quite handy! Thank you. – MarcoB Aug 19 '15 at 19:10

rhermans · Answer 3 · 2015-08-19T17:09:44.137

Example data

data = SortBy[RandomReal[1, {10, 2}], First]

{{0.20784, 0.522849}, {0.437556, 0.931183}, {0.468446, 0.86256}, {0.474691, 0.535952}, {0.52331, 0.838424}, {0.549898, 0.135879}, {0.686447, 0.670915}, {0.807457, 0.539869}, {0.829756, 0.267644}, {0.916977, 0.962118}}

As pointed by @march, if you have two lists, xList and yList, you can put them in the correct form by using Transpose

data=Transpose[{xList, yList}]]

To plot use ListPlot or ListLinePlot

ListLinePlot[data]

or

ListPlot[data, Joined->True]

Smoothness could be achieved using the option InterpolationOrder

ListPlot[data
 , InterpolationOrder -> 2
 , PlotRange -> All
 , Joined -> True
 ]

Scatter plot with smooth lines

3 Answers3