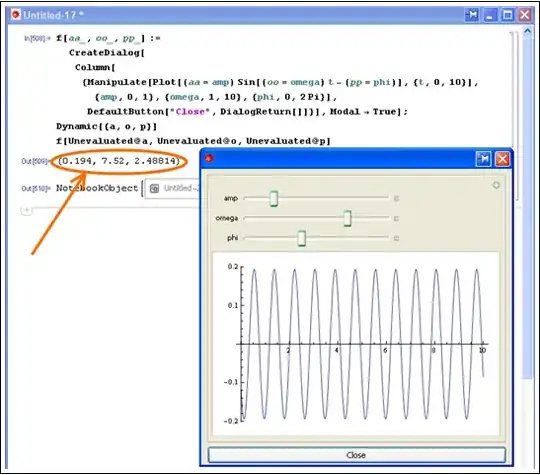
I have a function, pasted at the bottom, which I would like to encapsulate into a function that can be called, and the program would then run in a popup window, return the values energy, peaklocation and amplitude, then when the user is finished with the manipulate function, they'd press a done button and the popup window would close, returning the created data and the user to the workbook.
The issue is mainly that, while I can get a popup window to appear, I cannot seem to figure out how to get it to include manipulators. Is there any way to run the following as a function in a popup window, or am I better off simply getting it to save results to a file and running it manually?
Here's the code:
SetOptions[InputNotebook[], PrintPrecision -> 10]
filelocation = SystemDialogInput["FileOpen"];
rawfiledata = Import[filelocation, "Table"];
trimmedfiledata = Drop[rawfiledata, {1}, {2, 4}];
Manipulate[moveamt = movelength, {movelength, 1, 25, 1}]
DynamicWrapper["Select the left and right edges of the data",
mmdata = MovingAverage[trimmedfiledata, moveamt];]
minx = Min[mmdata[[All, 1]]];
minx = minx - 0.02;
maxx = Max[mmdata[[All, 1]]];
maxx = maxx + 0.02;
miny = Min[mmdata[[All, 2]]];
maxy = Max[mmdata[[All, 2]]];
Manipulate[leftEdge = left, {left, minx, maxx, 0.001}]
Manipulate[rightEdge = right, {{right, maxx}, minx, maxx, 0.001}]
Manipulate[c1 = peak, {peak, minx, maxx, 0.001}]
Manipulate[yoff = floor, {floor, miny, maxy, 0.001}]
(*d1 is edges*)
Dynamic[d1 = Select[mmdata, leftEdge < #[[1]] < rightEdge &];]
Dynamic[Show[
ListPlot[mmdata, PlotStyle -> Orange,
GridLines -> {{{c1, Orange}, leftEdge, rightEdge}, {{yoff, Red}}}],
ParametricPlot[bsplinedat = BSplineFunction[mmdata][x], {x, -8, 8}],
ListPlot[d1, PlotStyle -> Purple], ImageSize -> Large]]
Dynamic[f1 =
NonlinearModelFit[d1, a Exp[-(b (x - c1))^2] + yoff, {a, b}, x]]
Dynamic[Show[{ListPlot[d1],
Plot[f1[x], {x, d1[[1, 1]], d1[[-1, 1]]}, PlotRange -> All]}]]
Dynamic[Show[{ListPlot[mmdata],
Plot[f1[x], {x, minx, maxx}, PlotRange -> All, PlotStyle -> Red]}]]
Dynamic[smooth2 = {#[[1]], #[[2]] - f1[#[[1]]]} & /@ mmdata;]
Dynamic[ListPlot[smooth2]]
Dynamic[energy = Integrate[Interpolation[mmdata][x], {x, minx, maxx}];]
Dynamic[peaklocation = c1;]
Dynamic[amplitude = f1[c1];]
b
Dynamic[s = 1/Sqrt[b]]
Dynamic[sd = StandardDeviation[d1]]
And here's some sample data, if needed for whatever reason: