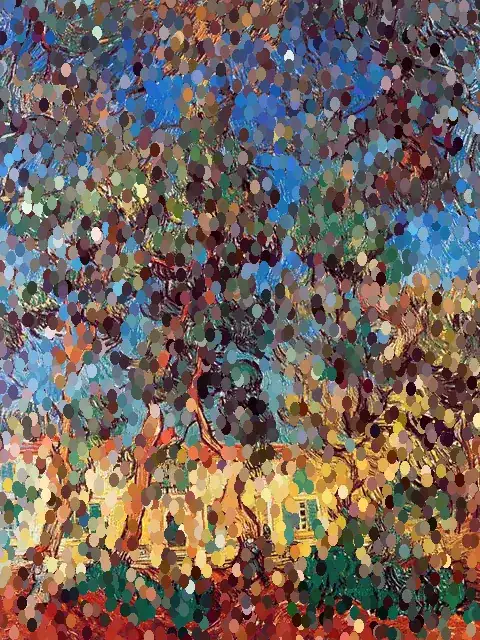Coloured image transformation in pointillism

Question

I would like to transform an image (a photo for example) into a set of single colour circles with fixed but adjustable diameter (bigger than the pixel size), into a kind of pointillism. The number of colours can be reduced. I tried to follow the examples in Artistic image vectorization, but I need to have divided circles rather than adjacent poligonal blocks. Final vectorisation will be more than welcome Thanks Virgilio

Answer 1

Here's one way to go about it. First choose an image (the view outside Van Gogh's asylum).

Define some auxiliary functions:

img = Import["https://i.stack.imgur.com/eMced.jpg"];
aspImg[im_] := ImageDimensions[im][[2]]/ImageDimensions[im][[1]];
imgSpheres[im_, diam_, numSphere_] := 
  Module[{r1, r2}, 
   colorfun = BSplineFunction[ImageData[im], SplineDegree -> 1];
   Graphics[
    Table[{r1, r2} = 
      RandomReal[{0, 1}, 2]; {RGBColor[colorfun[1 - r2, r1]], 
      Disk[{r1, r2}, diam]}, {i, 1, numSphere}], 
    AspectRatio -> aspImg[im], Axes -> False, ImageSize -> Large]];

Now call the function:

ImageCompose[img, {imgSpheres[img, 0.01, 3000], 1}]

The first argument to imgSpheres is the image, the second argument is the size of the circles, and the third is the number of circles to draw. The final argument allows some of the original image to show through by adjusting the opacity.

ImageCompose[{img, 1}, {imgSpheres[img, 0.02, 3000], 0.8}]

Answer 2

This works for version 9 (November 20, 2012). Make a Delaunay triangulation of random points laid down in the image, find the incircles of the triangles, and colour them by the underlying image. Placing more points results in smaller disks.

Graphics`Mesh`MeshInit[]
(* {"PacletManager`", "QuantityUnits`", "WebServices`",
    "System`","Global`", "Graphics`Mesh`"} *)

Incircle[{{x1_, y1_}, {x2_, y2_}, {x3_, y3_}}] := 
   With[{a = Norm[{x2 - x3, y2 - y3}], b = Norm[{x3 - x1, y3 - y1}], 
         c = Norm[{x1 - x2, y1 - y2}]}, 
        Circle[(a {x1, y1} + b {x2, y2} + c {x3, y3})/(a + b + c),   
           Sqrt[-(a - b - c) (a + b - c) (a - b + c)/(a + b + c)]/2]]

• image is a colour image, no transparency channel
• n is the number of points to place in the image
• s=-1 for more points in light areas, fewer in dark
• s=+1 for more points in dark areas, fewer in light
• e is an exponent for nonlinear colour scaling
• opts is a list of Graphics options

The above parameters are passed to the following function.

DelaunayImageColour[image_, n_, s_, e_, opts___] :=
   Block[{w, h, data, ij, p, gopt, rr, gg, bb},
         {w, h} = ImageDimensions[image];
         data = ImageData[ImageRotate[image, Right]];
         ij = Transpose[{RandomInteger[{1, w}, n], RandomInteger[{1, h}, n]}];
         p = Pick[ij, 
                  Sign[RandomReal[{0., 1.}, n] - 
                      (Extract[data, ij] /. {rr_, gg_, bb_} -> 
                      0.299 rr + 0.587 gg + 0.114 bb)], s];
         gopt = FilterRules[{opts}, Options[Graphics]];
         Graphics[
            Map[{Apply[RGBColor, Mean[Extract[data, Floor[#]]]^e], 
            Incircle[#]} &, Delaunay[p]] /. Circle -> Disk, gopt]]

For example,

   DelaunayImageColour[Import["VanGogh.jpg"], 100000, -1, 1.0, Background -> Black]

Answer 3

img = ExampleData[{"TestImage", "Lena"}];

Rotate[Graphics@
  Join[
   MapIndexed[
    {RGBColor[#1], Disk[4 Most@#2 + RandomReal[{-1, 1}, 2], 4]} &,
    ParallelTable[
     Table[
      Take[
        SortBy[Tally[
          Flatten[Map[Round[#, 0.01] &, ImageData[im], {2}], 1]], 
         Last], -1][[All, 1]]
      , {im, iml}]
     , {iml, ImagePartition[img, 20]}
     ], {3}],
   MapIndexed[
    {RGBColor[#1 + RandomReal[{-0.2, 0.3}, 3]], 
      Disk[Most@#2 + RandomReal[{-1, 1}, 2], Last@#2/10]} &,
    ParallelTable[
     Table[
      Take[
        SortBy[Tally[
          Flatten[Map[Round[#, 0.01] &, ImageData[im], {2}], 1]], 
         Last], -4][[All, 1]]
      , {im, iml}]
     , {iml, ImagePartition[img, 5]}
     ], {3}]], -\[Pi]/2]