I'm having some problems with Interpolation. I'm trying to interpolating some measurements data into mathematica. But using Interpolation will create some negative data, which is actually not possible in the real life.
For example, I'm trying to interpolate these data:
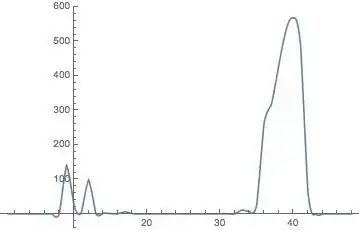
fct = Interpolation[{0, 0, 0, 0, 0, 0, 0, 0, 140.6833333, 24.58333333,
3.5, 98.86666667, 0.8, 2.233333333, 0.983333333, 0.466666667,
5.983333333, 0.583333333, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
11.5, 7.333333333, 27.13333333, 263.7833333, 316.9166667, 429.2,
532.4666667, 567.4833333, 486.4333333, 61.98333333, 0, 0, 0, 0, 0,
0}]
Then I try to visualize them
Plot[fct[i], {i, 1, 48}]
Only to find that there is a little part of the function that lies unter the x axis.
Is there any way to avoid this? Thank you all in advance!
{}button above the edit window. The edit window help button?is also useful for learning how to format your questions and answers. You may also find this this meta Q&A helpful – Michael E2 Aug 29 '15 at 18:56