n-dimensional plot

Question

I want to plot 6-dimensional data using parallel axes (https://en.wikipedia.org/wiki/Parallel_coordinates). The list looks like this:

    {{a1,b1,c1,d1,e1,f[a1,b1,c1,d1,e1]},{a2,b2,c2,d2,e2,f[a2,b2,c2,d2,e2]},{},...}

I need to draw six vertical axes with scales on them, connect the dots with lines, and color these lines according to the value of f[ai,bi,ci,di,ei], or the last coordinate.

A three dimensional example with two data would help me start, but I don't know how to do it.

Thank you.

Answer 1

Here's a start:

parallelPlot[dat_] := 
 ListPlot[dat, 
  Prolog -> 
   Table[Line[{{i, Min[dat]}, {i, Max[dat]}}], {i, 
     Length[dat[[1]]]}],
  PlotStyle -> 
   Table[Blend[{Red, Blue}, 
     Rescale[dat[[i, -1]], {Min[dat[[All, -1]]], Max[dat[[All, -1]]]}
      ]], {i, Length[dat]}],
  Joined -> True,
  Axes -> False
  ]

Test:

parallelPlot[RandomInteger[{-5, 5}, {10, 6}]]

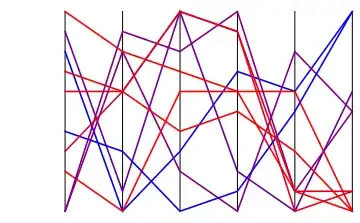
Things that one can easily add but I don't have time now:

1. Rescale each coordinate separately.
2. Ticks, labels, etc.
3. Colorbar

======= Better function, that also rescales ========

The Rescale function is what you should use for rescaling. Let's keep the minimum and maximum of each dimensions in the variables mins and maxs, and thus

{mins, maxs} = Transpose[{Min[#], Max[#]} & /@ Transpose[data]];
rescaledData = 
  Transpose@
   Table[Rescale[data[[All, i]], {mins[[i]], maxs[[i]]}], {i, Length@data[[1]]}];

We can then use mins and maxs to create tick labels at the bottom and top of each dimension. Here's the integrated code (I also added a Floor and Ceiling functions in the calculation of mins and maxs to make the bounds nicer):

parallelPlot[data_] := Block[{mins, maxs, rescaledData, n, ndim},
   n = Length[data];
   ndim = Length[data // First];
   {mins, maxs} = Transpose[{Floor@Min[#], Ceiling@Max[#]} & /@ Transpose[data]];
   rescaledData = 
    Transpose@
     Table[Rescale[data[[All, i]], {mins[[i]], maxs[[i]]}], {i, ndim}];
   ListPlot[rescaledData,
    Prolog -> Table[Line[{{i, 0}, {i, 1}}], {i, ndim}],
    PlotStyle -> Table[Blend[{Red, Blue}, rescaledData[[i, -1]]], {i, n}],
    Epilog -> {
     Table[Text[mins[[i]] // ToString, {i, 0}, {-1, 0}], {i, ndim}], 
     Table[Text[maxs[[i]] // ToString, {i, 1}, {-1, 0}], {i,ndim}]
    },
    Joined -> True, 
    Axes -> False];

To test, we generate 6-dimensional random data (here its 15 points), where each coordinate is randomly distributed between two random bounds.

d = Transpose@Table[
        RandomReal[{Min@#, Max@#} &@RandomInteger[{0, 10}, 2], 15],
    {6}]
parallelPlot@d

Answer 2

I took another stab at the problem to produce a self-contained function that generates axes as well as rescales the data. The function nplot is defined below. It takes a list of data as input

Clear[nplot]

nplot[data_?(ArrayQ[#, 2, NumericQ] &), ImageSize -> size_] := Module[
  {rescaled, plot, axes},
  rescaled = Transpose@(Rescale /@ Transpose@data);
  plot =
   ListLinePlot[
    rescaled, PlotRange -> {{1, Last@Dimensions@data}, Automatic},
    ImageSize -> size, PlotRangePadding -> None, Axes -> None
   ];
  axes =
   Map[
    ListPlot[
      data[[All, #]], PlotStyle -> None, 
      PlotRange -> {{1, Last@Dimensions@data}, Automatic},
      Axes -> {False, True}, PlotRangePadding -> None,
      ImageSize -> size, Background -> None, 
      AxesOrigin -> {#, Automatic}] &,
    Range[Last@Dimensions@data]
   ];
  Overlay[Flatten@{plot, axes}]
]

nplot[data_] := nplot[data, ImageSize -> Automatic]

Within nplot I generate a column-wise rescaled version of the data that is plotted using ListLinePlot; the axes of this plot are suppressed, because they will be replaced by more appropriate ones reflecting the non-rescaled value of the variables. I then use the existing ListPlot machinery to generate appropriately scaled and placed axes for the non-rescaled data, which are stored in axes within nplot. Finally, the rescaled plot and non-rescaled axes are overlaid and returned.

The function checks the nature of the input data (it must be at least a 2-dimensional array: a vector would result in a straight line across the plot and would be very uninteresting) and passes through values of the ImageSize option, if set by the user (otherwise a value of Automatic is used).

---

Here is what the function produces with some random input:

SeedRandom[123]
pts = RandomReal[{-10, 10}, {15, 6}];
nplot[pts, ImageSize -> Large]