I am given the Legendre expansion of the first kind. $$f(x)=\sum_{n=0}^{\infty}A_{n}P_{n}(x).$$
I have worked the coefficient to be $$A_{n}=\frac{1}{\left \| P_{n}(x) \right \|^{2}} \int_{x=-1}^{x=1}f(x)P_{n}dx $$
Here are my codes:
The function f is also given. I'm trying to sum the expression as outlined. How should I go about implementing some kind of loop?
When your book refers to the norm of the Legendre polynomials it is using the $L^2$ norm, because the orthogonality relationship is
$$ \int_{-1}^{1} P_m(x) P_n(x) dx = \frac{2}{(2 m+1)} \delta_{mn} $$
So,
f[x_] := x^3 - 4 x^2 + 4 x + 2
a[m_, f_] := a[m, f] = (2 m + 1)/2 Integrate[LegendreP[m, x] f[x], {x, -1, 1}]
Manipulate[
k = Sum[a[m, f] LegendreP[m, #], {m, 0, i}] &;
Plot[{k[t], f[t]}, {t, -1, 1}, PlotLabel -> "Order: " <> ToString@i],
{i, 0, 5, 1}]
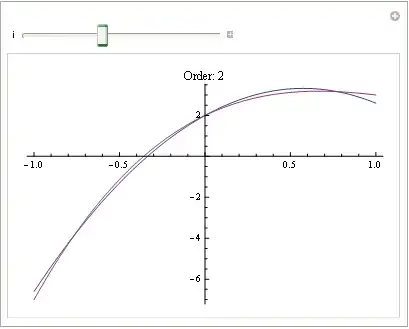
Another example:
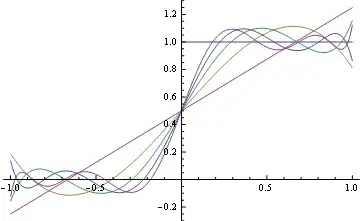
f[x_] := UnitStep[x]
a[m_, f_] := a[m, f] = (2 m + 1)/2 Integrate[LegendreP[m, x] f[x], {x, -1, 1}]
k = Sum[a[m, f] LegendreP[m, #], {m, 0, i}] &;
Plot[Evaluate@Join[{f[t]}, Table[k[t], {i, 1, 9, 2}]], {t, -1, 1}, PlotRange -> All]
&at the end, forming a function/argument pair. See for example this answer, and all the other answers in that question too, BTW. – Dr. belisarius Sep 03 '15 at 12:58k = Function[{s}, Sum[a[m, f] LegendreP[m, s], {m, 0, i}]]– Dr. belisarius Sep 03 '15 at 13:11