Solve simple trig equation

Question

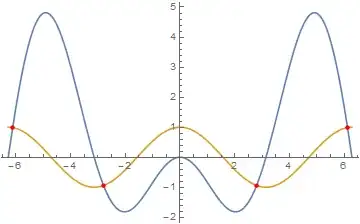
I would like to solve this equation:

$$-x\sin(x)=\cos(x)$$

But Solve in Mathematica doesn't work:

This system cannot be solved with the methods available to Solve

Being a beginner, I don't know any other ways to solve this equation. Any suggestions?

Thanks!

Have a look at NSolve, which solves an equation numerically. — sacratus, Sep 03 '15 at 07:53

score 16 · Accepted Answer · answered Sep 03 '15 at 08:06

16

Restrict the domain:

Solve[-x Sin[x]==Cos[x]&&-30<=x<=30,x,Reals]//N

{{x->-28.2389},{x->-25.0929},{x->-21.9456},{x->-18.7964},{x->-15.6441},{x->-12.4865},{x->-9.31787},{x->-6.12125},{x->-2.79839},{x->2.79839},{x->6.12125},{x->9.31787},{x->12.4865},{x->15.6441},{x->18.7964},{x->21.9456},{x->25.0929},{x->28.2389}}

answered Sep 03 '15 at 08:06

ciao

25,774
2
58
139

7

As long as you're adding the constraint -30<=x<=30, the 3rd argument Reals is superfluous. – murray Sep 03 '15 at 14:59
For me, restricting to the Reals is more useful than constraining the domain. – Ron Jensen Jun 20 '20 at 23:40

score 4 · Answer 2 · answered Sep 03 '15 at 07:58

4

FindRoot[x Sin[x] == -Cos[x], {x, 2}]

gives

(* {x -> 2.79839}  *)

answered Sep 03 '15 at 07:58

thils

3,228
2
18
35

score 4 · Answer 3 · answered Sep 03 '15 at 09:46

In which domain do you want to solve your problem? Make a plot and restrict your domain (example here [-2 Pi,2 Pi]).

sol = x /. NSolve[-x Sin[x] == Cos[x] && -2 \[Pi] < x < 2 \[Pi], x]
{-6.12125, -2.79839, 2.79839, 6.12125}

Plot[{-x Sin[x], Cos[x]}, {x, -2 \[Pi], 2 \[Pi]}, 
 Epilog -> {Red, PointSize -> Medium, Point[{#, Cos[#]} & /@ sol]}]

score 2 · Answer 4 · answered Aug 29 '17 at 15:46

2

Another function worth trying in cases like this may be FindInstance:

FindInstance[-x Sin[x] == Cos[x], x] // N
{{x -> 2.79839}}

If you want more answers:

FindInstance[-x Sin[x] == Cos[x], x, 3] // N

answered Aug 29 '17 at 15:46

bill s

68,936
4
101
191

score 1 · Answer 5 · answered Aug 29 '17 at 13:21

The function cotSol[k, λ] for generating the $k$-th positive root of $\lambda x=\cot x$, which I wrote for this answer, can be used to directly generate the required solutions:

N[cotSol[Range[10], -1], 20]
   {2.7983860457838871367, 6.1212504668980683013, 9.3178664617910653790,
    12.486454395223781428, 15.644128370333027630, 18.796404366210157169,
    21.945612879981044573, 25.092910412112097360, 28.238936575260272929}

The negative roots are of course just the negations of the positive roots in this case.

Solve simple trig equation

5 Answers5

Linked

Related