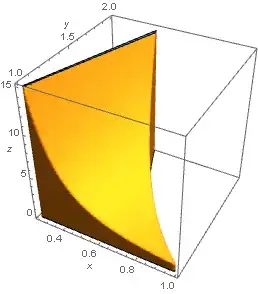
Consider the following region:
eq1 = 4 x;
eq2 = 1/x;
eq3 = 1;
cover = y^2/x^2;
bottom = eq3 < y < eq1 && eq3 < y < eq2;
reg3D = ImplicitRegion[bottom && 0 <= z <= cover, {{x, 1/4, 1}, {y, 1, 2}, {z, 0, 15}}];
RegionPlot3D[bottom && z < cover, {x, 1/4, 1}, {y, 1, 2}, {z, 0, 15},
PlotPoints -> 100, Mesh -> None, AxesLabel -> Automatic]
When I discretize this solid, I get the error messages:
DiscretizeRegion[reg3D, AccuracyGoal -> 4]
DiscretizeRegion::drf: DiscretizeRegion was unable to discretize the region ImplicitRegion[<<2>>].
BoundaryDiscretizeRegion[reg3D, AccuracyGoal -> 4]
BoundaryDiscretizeRegion::drf: "BoundaryDiscretizeRegion was unable to discretize the region ImplicitRegion[<<2>>]."
An attempt with "NDSolveFEMToElementMesh" terminates the C-Compiler.

Reducing the z domain 0 < z < 9.7; all works fine.
new3D = ImplicitRegion[bottom && 0 <= z <= cover, {{x, 1/4, 1}, {y, 1, 2}, {z, 0, 9.7}}];
DiscretizeRegion[new3D, AccuracyGoal -> 4]
BoundaryDiscretizeRegion[new3D, AccuracyGoal -> 4]
I am looking for a technique to discretize the whole solid with 0 < z < 15?

[text](url). – Michael E2 Sep 08 '15 at 16:41DiscretizeRegionis roughly equivalent toDiscretizedGraphics@RegionPlot..., at least for the default settings. So if there's a problem, it's notDiscretizeRegionvs.DiscretizeGraphics. The volume problem, which is distinct from the question you asked here, seems to be the same problem as in your previous question, a degenerate polygon. – Michael E2 Sep 08 '15 at 17:10