Find Maximum doesn't seem to work

Question

r[t_] = {3 Cos[(3.3)*π*t], Sin[4*π*t] + 4 t};
n[t_] = Norm[r'[t]*r''[t]]/Norm[r'[t]];
Plot[n[t], {t, 0, 1}, 
  PlotLabel -> "Normal Component of Acceleration vs Time", 
  AxesLabel -> {"Time (hours)", "Acceleration (km/h^2)"}]
FindMaximum[n[t], {t, 0}]

I'm trying to find the maximum of the curve n[t], but when using FindMaximum, the value that is returned clearly doesn't fit the graph.

What happens if you try FindMaximum[n[t], {t, .075}]. I get {221.359, {t ->0.0605467}}, which appears to be the first maximum of n[t] to the right of zero. — m_goldberg, Sep 17 '15 at 01:43
I'm voting to close this question as off-topic because it is too specific — yohbs, Sep 17 '15 at 06:20
possible duplicate of How to find all the local minima/maxima in a range — xyz, Sep 18 '15 at 02:08

score 6 · Answer 1 · answered Sep 17 '15 at 08:09

Try the option Method -> "PrincipalAxis". In your case these are your functions:

 r[t_] = {3 Cos[(3.3)*\[Pi]*t], Sin[4*\[Pi]*t] + 4 t};
n[t_] = Norm[r'[t]*r''[t]]/Norm[r'[t]];

Here are the maxima coordinates within the interval (0, 0.5):

    coord1 = {#[[2, 1, 2]], #[[1]]} &[
  FindMaximum[n[t], {t, 0.1}, Method -> "PrincipalAxis"]]

coord2 = {#[[2, 1, 2]], #[[1]]} &[
  FindMaximum[n[t], {t, 0.2}, Method -> "PrincipalAxis"]]

coord3 = {#[[2, 1, 2]], #[[1]]} &[
  FindMaximum[n[t], {t, 0.4}, Method -> "PrincipalAxis"]]

and this is the visualization:

Show[{
  Plot[n[t], {t, 0, 0.5}, 
   PlotLabel -> "Normal Component of Acceleration vs Time", 
   AxesLabel -> {"Time (hours)", "Acceleration (km/h^2)"}],
  Graphics[{Red, PointSize[0.03], Point[coord1], Green, Point[coord2],
     Magenta, Point[coord3]}]
  }]

yielding this:

Have fun!

Had a very similar problem and this change in Method solved it. I disliked it a bit because I had to omit the constraints. So the solution felt a bit frail. Still, +1 for a working solution :) — ivbc, Jun 21 '16 at 02:21

score 3 · Answer 2 · edited Apr 13 '17 at 12:55

Using FindAllCrossings from here

norm[x_List] := Sqrt[x.x] (* Norm[ ] is always problematic *)
r[t_] := {3 Cos[3.3 π t], Sin[4 π t] + 4 t};
n[t_] := norm[r'[t] r''[t]]/norm[r'[t]];

(* now we find the extremes using the derivative and get the global max *)
max = Last@SortBy[{#, n@#} & /@ FindAllCrossings[n'[t], {t, 0, 1}], Last]
Plot[n[t], {t, 0, 1}, Epilog -> {PointSize[Large], Red, Point@max}]

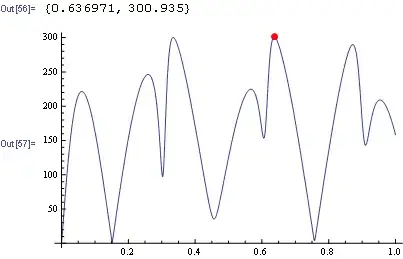
Mathematica graphics

These are all the extrems:

ms = SortBy[{#, n@#} & /@ FindAllCrossings[n'[t], {t, 0, 1}], -Last[#] &]

{{0.636971, 300.935}, {0.33428, 300.114}, {0.871933, 289.731}, 
 {0.259015, 246.272}, {0.567049, 224.732}, {0.0605467, 221.359}, 
 {0.95363, 209.144}, {0.605623, 153.361}, {0.910354, 143.132}, 
 {0.302482, 97.1912}, {0.456713, 35.638}, {0.757384, 3.91173}, {0.151483, 0.516416}}

pt = {#, n@#, Sign[n''@#]} & /@ FindAllCrossings[n'[t], {t, 0, 1}]
Plot[n[t], {t, 0, 1}, 
     Epilog -> {PointSize[Large], 
                Red, Point@Cases[pt, {x__, 1} :> {x}], 
                Green, Point@Cases[pt, {x__, -1} :> {x}]}]

Mathematica graphics

Find Maximum doesn't seem to work

2 Answers2

Linked