What is the syntax to add a vector v1 to each vector in a list of vectors v2?
I know it has to be simple, but I really have searched and not found it.
v1 = {a, b, c}
v2 = {{d, e, f}, {g, h, i}, {j, k, l}}
i.e., sum them in a way to give:
{{a + d, b + e,c + f}, {a + g, b + h, c + i}, {a + j, b + k, c + l}}
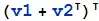
Innerisn't well enough entrenched yet. I failed to notice that myInnereffectively simplified toTranspose @* Plus! – Patrick Stevens Sep 19 '15 at 22:28Transposeall the time - for intuitive clarity and readability, sometimes one can get faster performance usingPartandAllin its place ... just FYItestData = Table[{{i, 2 i}, 3 i}, {i, 1000000}]; Print@Timing[ Length[ Last[ Transpose[testData]]]]; Print@Timing[ Length[ Part[ testData, All, 2]]]; Print@Timing[ Length[ testData[[ All, 2]]]];– Mark Samuel Tuttle Sep 23 '15 at 13:32