I would like to plot the temperature distribution for a particular case. the problem is stated in the paper, behind a paywall here, summarized as
Consider a one-dimensional container of length l, full of liquid with a freezing temperature $T_m$. Suppose the initial temperature of the liquid $T_L$ is higher than $T_m$, and one end of the liquid x = 0 is maintained at temperature $T_S$ (< $T_m$) for t > 0, whereas the other end $x = l$ is insulated. The solidification process consequently starts from $x = 0$, and extends over increasing intervals as the time $t$ increases (a well-known Stefan problem). We assume that the material density $\rho$ is constant; and the thermophysical properties are the latent heat $L$, the respective specific heats of the liquid and solid $c_L$ and $c_S$, and the respective thermal conductivities of the liquid and solid $k_L$ and $k_S$.
The initial and boundary conditions are given by,
The temperature distribution follows
where $E(x,t)$ is the enthalpy at time $t$ and position $x$. The enthalpy at time zero is $$E(x,0) = \rho c_L (T_L-T_m) + \rho L$$
and for later times is given by
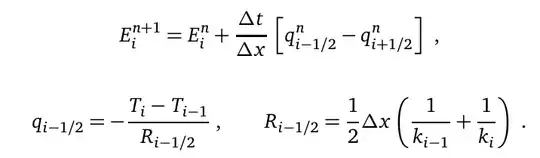 Taking $T_L=37^\circ \mathrm{C}$, $T_S=-200^\circ \mathrm{C}$, and $l=0.1\mathrm{m}$, and the other constants defined below, how can I calculate the temperature distribution using Mathematica?
Taking $T_L=37^\circ \mathrm{C}$, $T_S=-200^\circ \mathrm{C}$, and $l=0.1\mathrm{m}$, and the other constants defined below, how can I calculate the temperature distribution using Mathematica?
Where is the problem? If I'd like to have a temperature (T) distribution at t=1000s, then i need data at t=999s. Which makes it quite awkward to write code in Mathematica. Can anyone help me on this?
This is the work I have done so far:
Clear["Global`*"];
T[i_, n_] :=
If[En[i, n] <= 0,
Tm + En[i, n]/(ρ cs),
If[0 < En[i, n] < ρ L, Tm,
If[ρ L <= E[i, n],
Tm + (En[i, n] - ρ L)/(ρ cl)]]]
En[i_, n_ + 1] :=
En[i, n + 1] =
En[i, n] + Δt/Δx*(-ks (
T[i, n] - T[i - 1, n])/Δx -
kl (T[i, n] - T[i + 1, n])/Δx)
T[0, n_] := T1[t] /. t -> n Δt;
M = 5;
T[M, n_] := T2[t] /. t -> n Δt;
T[i_, 0] := T0[x] /. x -> i Δx
En[i_, 0] := ρ cl (T1[0] - Tm) + ρ L;
L = 0.1; ks = 0.00266; kl = 0.006; \
cs = 1.7; cl = 4.1868; ρ = 1000;
Δt = 0.1; Δx = L/M; Tm = 0;
T0[x_] = -200;
T1[t_] = 37;
T2[t_] = -200;
Table[ListPlot[Table[{Δx i, T[i, n]}, {i, 0, M}],
PlotJoined -> True, PlotRange -> {0, 0.4}, AxesLabel -> {"x", ""},
PlotLabel -> "T[x,t], t=" <> ToString[Δt n]], {n, 0,
80, 20}]
Would it be possible to model both types of phase transitions - not just freezing but also melting?
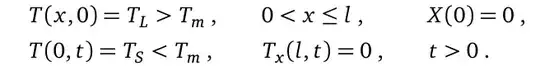
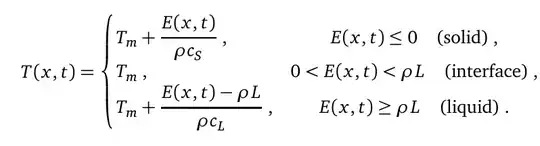


L- do you have it divided into subsections? If so, how many? What are E and rho? Both E and T have two different forms - a continuous form, $E(x,t)$ and $T(x,t)$, and a form with sub and superscripts - $E^n_i$ and $T^n_i$. How are they related? You also have $T_m$. Be more explicit, or provide a link to where the problem is laid out in more detail. – Jason B. Sep 24 '15 at 09:05NDSolve? – george2079 Sep 24 '15 at 12:09Nest[ <code to update E,T> , <initial E> , num time steps ]. (This is the point of an explicit scheme you don't need to solve simultaneously for all time at once ) – george2079 Sep 24 '15 at 14:07