Here's one approach, attempting to find a sufficiently good local maximum for minimum color difference of ten colors differing from black and white, and each other:
Module[
{sRGB, toLCH, oldcolors, ncolors, newcolorvars, newcolors, allcolors},
sRGB = Import["sRGB_v4_ICC_preference.icc"];
toLCH = ColorConvert[#, sRGB -> "LCH"] &;
oldcolors = {Black, White};
ncolors = 10;
newcolorvars = Array[c, {ncolors, 3}];
allcolors = Join[oldcolors, newcolorvars];
newcolors = RGBColor @@@
(newcolorvars /. Last@Quiet@NMaximize[
Min[
ColorDistance[toLCH@#1, toLCH@#2,
DistanceFunction -> "CIE2000"] & @@@
Subsets[allcolors, {2}]],
Flatten@newcolorvars \[Element]
Cuboid[Table[0, {3 ncolors}]],
Method -> "SimulatedAnnealing",
MaxIterations -> 1000000000]);
Join[oldcolors, newcolors]]
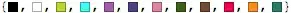
Pairwise comparison visualization of selected colors:
Table[Graphics@{Circle[],
Table[{#[[i]],
Disk[{0, 0},
1, \[Pi]/2 - (2 \[Pi]/Length@#) {i - 1, i}]}, {i,
Length@#}] &@#, {i, Disk[{0, 0}, 2/3]}}, {i, #}] &@%

There are multiple problems in this implementation:
ColorDistance seems to require unexplained pre-conversion to LCH colorspace to work acceptably. In general, there's something deeply disturbing in colorspace handling Mathematica does - or doesn't seem to do, sometimes. Linear and non-linear colorspaces are not intuitively separate, or compatible, for instance.NMaximize has trouble trying to find good maxima because ColorDistance is only numeric and the domain has lots of local maxima.ColorDistance functions in general are not even meant to perform large color separation measures, but rather ones very close to a reference color. (Related commentary: Is ColorDistance symmetric?)Min is not necessary a sensible aesthetic metric. Something like Mean@# / Variance@# & might make more sense, but is takes forever in practice.
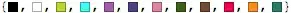

Table[ColorData["BrightBands"][i], {i, 0, 1, .1}]There are a number of both continuous and discrete sets. – Andy Ross Sep 29 '15 at 13:09ColorDistancefunction with a sufficiently good polynomial approximation, possibly optimized specifically for suprathreshold color difference measure (built-in color distance functions are really designed to measure perceptual "sameness" acceptability of colors, for instance for manufacturing and other reprocution purposes). I suspect this could drastically speed up computation of color groups. – kirma Sep 30 '15 at 07:47