How can I illustrate the solution space of these equations in 3D?

Question

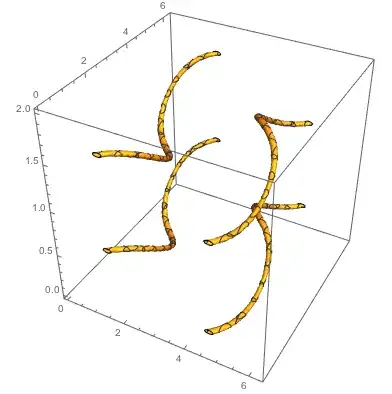
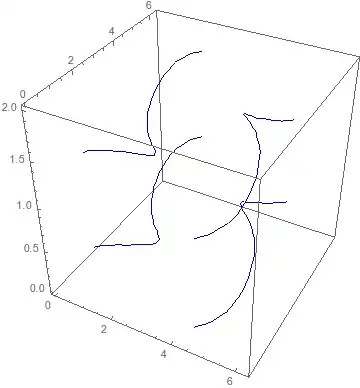
I would like to plot the solution space $\{\theta,\varphi,\Omega\}$ of this vector equation,

$$\begin{pmatrix} \sin (\theta ) \sin (\varphi ) \sin (2 \pi \Omega )-\sin (2 \theta ) \cos (\varphi ) \sin ^2(\pi \Omega )\\ -2 \sin (\theta ) \sin (\pi \Omega ) (\cos (\theta ) \sin (\varphi ) \sin (\pi \Omega )+\cos (\varphi ) \cos (\pi \Omega )) \\ -\sin ^2(\theta ) \cos (2 \pi \Omega )-\cos ^2(\theta ) \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$$

In mathematica I tried to use Solve and use ParametricPlot3D,

Solve[
  {-Cos[φ] Sin[2 θ] Sin[π Ω]^2 + Sin[θ] Sin[φ] Sin[2 π Ω], 
   -2 Sin[θ] Sin[π Ω] (Cos[φ] Cos[π Ω] + Cos[θ] Sin[φ] Sin[π Ω]), 
   -Cos[θ]^2 - Cos[2 π Ω] Sin[θ]^2} == {0,1,0},{θ, φ, Ω}]

However, Solve gives me too many solutions (including complex) such that I don't have a simple way to handle them.

I roughly know that the solution space should be a spiral curve.

In general, given such a vector equation, how would I plot the solution space in 3D?

Answer 1

For any given theta, you have a curve in phi/omega space. Thus, one way to visualize this is to plot in the phi/omega plane over all theta:

sol = Solve[{-Cos[φ] Sin[2 θ] Sin[π Ω]^2 + Sin[θ] Sin[φ] Sin[2 π Ω],
        -2 Sin[θ] Sin[π Ω] (Cos[φ] Cos[π Ω] + Cos[θ] Sin[φ] Sin[π Ω]), 
        -Cos[θ]^2 - Cos[2 π Ω] Sin[θ]^2} == {0, 1, 0}, {θ, φ, Ω}];
Plot[sol[[All, All, 2]], {θ, 0, Pi}]

Plotting over a larger set of theta values:

Plot[sol[[All, All, 2]], {θ, 0, 4 Pi}]

And here it is in 3D:

ListPointPlot3D[Flatten[Abs[
   Table[Table[Flatten[{θ, sol[[All, All, 2]][[i]]}], {i, 16}], 
        {θ, 0.01, Pi, 0.001}]], 1]]

Answer 2

It seems you don't need the other two equations, the second one by itself defines the curves:

ContourPlot3D[
 -2 Sin[θ] Sin[π Ω] (Cos[φ] Cos[π Ω] + Cos[θ] Sin[φ] Sin[π Ω]) == 0.99,
 {θ, 0, 2 π}, {φ, 0, 2 π}, {Ω, 0, 2},
 PlotPoints -> 100, MaxRecursion -> 0]

Another way to do it is to use Maxim Rytin's BoundaryStyle trick as described by Daniel Lichtblau:

{f, g, h} =
 {-Cos[φ] Sin[2 θ] Sin[π Ω]^2 + Sin[θ] Sin[φ] Sin[2 π Ω], 
 -2 Sin[θ] Sin[π Ω] (Cos[φ] Cos[π Ω] + Cos[θ] Sin[φ] Sin[π Ω]), 
 -Cos[θ]^2 - Cos[2 π Ω] Sin[θ]^2};
ContourPlot3D[
 Evaluate@{f == 0, h == 0},
 {θ, 0, 2 π}, {φ, 0, 2 π}, {Ω, 0, 2}, 
 RegionFunction -> Function[{θ, φ, Ω}, Evaluate[g > 0]], 
 BoundaryStyle -> {1 -> None, 2 -> None, {1, 2} -> Darker@Blue}, 
 ContourStyle -> None, Mesh -> None, PlotPoints -> 20, MaxRecursion -> 0]

This plots the curves defined by the conjunction of the first and third equations. The RegionFunction eliminates the extra curves corresponding to the second equation being $-1$.

This approach can more easily handle different values of the right-hand side. For example, for $(1/\sqrt2,1/\sqrt2,0)^T$ you can just replace the first argument of ContourPlot3D with Evaluate@{f == 1/Sqrt@2, h == 0}.