10

Is there a built-in way to define a 3D region from an arbitrary list of points. The points will represent vertices of the edges of the region and we can assume that 1) they are not all on the same plane and 2) that there are at least 4 points. The points should define the region that allow the biggest volume given the provided vertices. I imagine something like Polygon except for 3 dimensional regions.

It needs to be a Mathematica region - something that I could use with functions like RegionIntersection or Volume. I have provided a list of example points below along with a (crude) picture of the volume I would like to derive from them, which I made manually. I am not necessarily interested in this volume in particular (it is just an example). I am mainly wondering if there is a generic method for any set of points

 points = {{0, 0, 1}, {5, 0, 0}, {1, 3, 0}, {0, 0, 2}, {4, 3, 0}, 
           {5, 0, 2}, {1, 3, 2}, {4, 3, 2}}

VolumePicture

corey979
  • 23,947
  • 7
  • 58
  • 101
BenP1192
  • 934
  • 6
  • 13
  • 2
    You can create a region for arbitrary 3D points with DelaunayMesh and/or MeshRegion . Unfortunately, RegionIntersection does not work with 3D MeshRegion objects. (This is mentioned in the section "Possible Issues" for RegionIntersection.) This command finds the volume of the 3D region over the points in the question: RegionMeasure[DelaunayMesh[points]]. – Anton Antonov Oct 05 '15 at 03:12
  • @AntonAntonov do you know any way to extract part from DelaunayMesh@points? The FullForm[DelaunayMesh@points] shows a lot of information but I can't extract any thing like I do with Graphics3D. Thank you – Basheer Algohi Oct 05 '15 at 04:11
  • @Algohi You can use MeshCells and MeshCoordinates. For example, look into the output of MeshCells[DelaunayMesh[points], 2] . – Anton Antonov Oct 05 '15 at 04:14
  • @AntonAntonov I know MeshCells and thank you for that but what I meant is when you look at FullForm[DelaunayMesh@points] I want for example to get the first list inside MeshRegion (Cases[DelaunayMesh@points,MeshRegion[x_,__]:>x]) or what is insde Tetrahedron (Cases[DelaunayMesh@points,MeshRegion[_,x_,__]:>x]) and so on. I can't use these methods because MeshRegion is Atomic expression and I cannot find a way to do that. – Basheer Algohi Oct 05 '15 at 04:25
  • @AntonAntonov Thanks you. Do you know if the 3-dimensional mesh primitives from a DelaunayMesh are guaranteed to be a set of Mathematica regions? For example, I was able to do RegionUnion @ MeshPrimitives[DelaunayMesh[points], 3] for this example, but I didn't know if this would be a solution in every case. Can you think of a case where this would not work? – BenP1192 Oct 05 '15 at 05:10
  • It seems that @BenP1192 asks not about mesh regions, but about regular regions. Am I right? If not, why not to use ToBoundaryMesh and ToElementMesh functions? They solve exactly such a task. – Alexei Boulbitch Oct 05 '15 at 07:52
  • @AlexeiBoulbitch I think you are right -- the question is not about mesh regions. That is why I posted a comment not an answer (talking about creating MeshRegion objects from points). – Anton Antonov Oct 05 '15 at 11:49
  • @BenP1192 I was not able to get a region with the command RegionUnion@MeshPrimitives[DelaunayMesh[points], 3] using the points defined in the question. – Anton Antonov Oct 06 '15 at 02:30

1 Answers1

12
points = {{0, 0, 1}, {5, 0, 0}, {1, 3, 0}, {0, 0, 2}, {4, 3, 0}, {5, 
    0, 2}, {1, 3, 2}, {4, 3, 2}};

reg = ConvexHullMesh @ points

enter image description here

RegionDimension @ reg

3

Volume @ reg
 (* or *)
RegionMeasure @ reg

21.5

p1 = {2.6161, 2.60692, 0.880247};
RegionMember[reg, p1]

True

p2 = {0.915295, 0.507214, 0.367796};
RegionMember[reg, p2]

False

RegionCentroid @ reg

{2.61628, 1.44767, 1.08721}

Integrate[x y z, {x, y, z} ∈ reg]

82.0625

RegionIntersection, RegionUnion etc. all have in their documentation (under Possible Issues) that they are "not implemented for MeshRegion objects embedded in 3D" and "nor for BoundaryMeshRegion objects embdedded in 3D". My idea is to triangulate the MeshRegion into Tetrahedrons and RegionUnion them into the desired Region:

tri = TriangulateMesh[reg, MaxCellMeasure -> Infinity];
pts = MeshCoordinates @ tri;
ord = Cases[Show[tri][[1]], Tetrahedron[x_] :> x, Infinity] // First;
tetra = Tetrahedron /@ (pts[[##]] & /@ ord);
Volume /@ tetra // Total

21.5

The volume agrees.

r = RegionUnion[tetra];
RegionPlot3D @ r

enter image description here

Volume @ r

21.4583

The volume slightly diverges from the correct value. Nevertheless:

ball = Ball[{0, 0, 1}];
RegionPlot3D @ (int = RegionIntersection[r, ball])

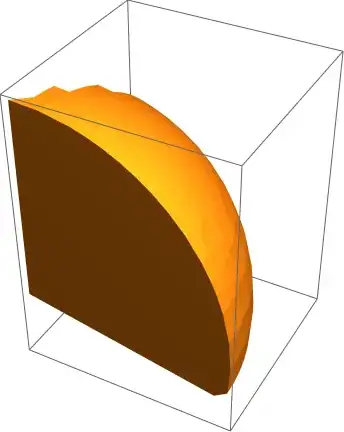
enter image description here

Volume @ DiscretizeRegion @ int

0.530894

I want to check how accurate is the volume measurement of int.

I start with altered points:

points1 = {{0, 0, 0}, {5, 0, 0}, {1, 3, 0}, {0, 0, 2}, {4, 3, 0}, {5, 
    0, 2}, {1, 3, 2}, {4, 3, 2}};

where I changed the first point - {0, 0, 1} - to {0, 0, 0}. Next I played with it forcefully

{b1, t1} = GatherBy[points1, Last];
ord = Drop[#, -1] & /@ (Flatten[#, 1] & /@ 
      FindCurvePath /@ {b1, t1}) // First;

to create the correct ordering for making

hex = Hexahedron @ Join[b1[[ord]], t1[[ord]]];

which has

Volume @ hex

24

I then take manually

b2 = {{1, 3, 0}, {5, 0, 0}, {0, 0, 0}, {0, 0, 1}};

for creating the chunk additially added to the above hex:

tetra = Tetrahedron @ b2;

These two can be handled with

Volume @ (region = RegionDifference[hex, tetra]) // N

21.5

to create the initial region of interest. Because this is a Region, one can

ball = Ball[{0, 0, 1}];
RegionPlot3D[#, PlotPoints -> 100]& @ (inter = RegionIntersection[region, ball])

enter image description here

(and do other Region* functions on it).

Volume @ N @ inter

0.534992

So the two measurements of the volume agree with each other.

corey979
  • 23,947
  • 7
  • 58
  • 101