Shading a region where an inequality is satisfied

Question

Bug introduced in 9.0 or earlier and persisting through 11.0.1 or later

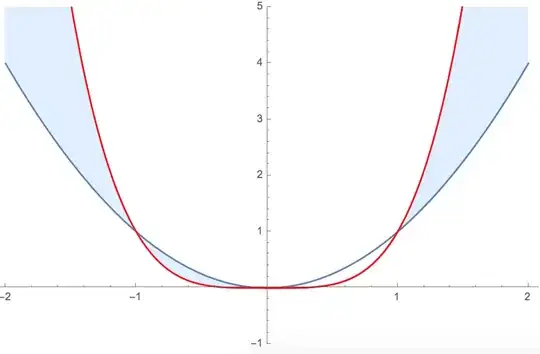
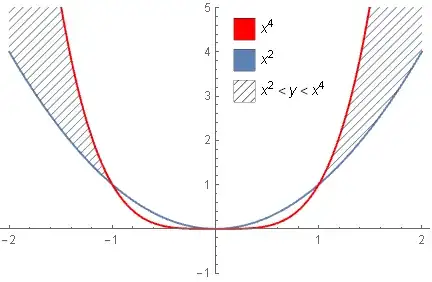
I'm creating solution sets for a calculus course and need to shade the region in $\mathbb R^2$ such that $x^2 < y < x^4$. This is what I have so far:

Plot[{x^2,x^4}, {x, -2, 2},PlotRange->{-1,5},PlotStyle->{Automatic,Red},
     Filling->{1->{{2},{LightBlue,White}}}]

Unfortunately this gives me the following picture. In particular, the region in the interval $(-1,0)$ is shaded. How can I avoid this?

This looks like a duplicate but it isn't. The issue here is that the OP is using the correct syntax, but the filling is nevertheless incorrect (possibly caused by the curves touching at 0 but not crossing). Looks like a bug to me. I guess a workaround may be to lower the x^2 function a tiny bit. — Sjoerd C. de Vries, Oct 07 '15 at 07:03

Sjoerd C. de Vries · Accepted Answer · 2015-10-07T10:23:30.420

9

As I stated in my comment below the post, the filling syntax used by the OP is correct. The behavior seen in the plot is a bug.

A workaround is to simply increase the number of plot points. The following works:

Plot[{x^2, x^4}, {x, -2, 2}, 
    PlotRange -> {-1, 5}, PlotStyle -> {Automatic, Red}, 
    Filling -> {1 -> {{2}, {LightBlue, White}}}, 
    PlotPoints -> 100
]

Mathematica graphics

Update

Actually, it is not a small plot point number that seems to be the cause. Depending on the PlotPoint setting two of the four areas are either incorrectly filled or incorrectly not filled. The following plot shows the filling of those areas as a function of the PlotPoint value (1 is filled, 0 is not filled):

Mathematica graphics

edited Oct 07 '15 at 10:23

answered Oct 07 '15 at 09:45

Sjoerd C. de Vries

65,815
14
188
323

Aha, nice catch +1. – Oct 07 '15 at 10:02
There will be an update. There's more to it. – Sjoerd C. de Vries Oct 07 '15 at 10:03
You beat me to your update: http://i.stack.imgur.com/O6ojv.gif. There's an interesting "discontinuity" at 49 and 53 plot points. The x^2 curve jumps to the x^4 for a point or two at x == 1. – Michael E2 Oct 07 '15 at 10:27
@Michael Yes, I noted that as well. Do you agree that we can tag this question with the "bugs" tag? Also, can I use your animation as an additional illustration? – Sjoerd C. de Vries Oct 07 '15 at 10:30
Yes, I think it's a bug. – Michael E2 Oct 07 '15 at 10:32

score 6 · Answer 2 · answered Oct 07 '15 at 06:57

6

Since Filling shades between two curves in the plot, add an extra curve that serves as the limit.

How about

Plot[{Max[x^2, x^4], x^2, x^4}, {x, -2, 2}, Filling -> {1 -> {2}}, 
PlotRange -> {-1, 5}]

To remember

Plot[{Min[x^2, x^4], x^2, x^4}, {x, -2, 2}, Filling -> {1 -> {2}}, 
PlotRange -> {-1, 5}]

answered Oct 07 '15 at 06:57

Aha! A clever trick indeed. Thanks! – user217285 Oct 07 '15 at 07:04

Syed · Answer 3 · 2024-01-13T04:13:16.913

Using Region* functionality:

The advantages of this approach are that one does not need to include additional curves to fill in the desired region and the description of the region is mathematical. The downside is that using Region commands may be accompanied with their own challenges.

Clear["Global`*"];
reg = ImplicitRegion[x^2 < y < x^4, {{x, -2, 2}, {y, -1, 5}}];
p1 = Plot[{x^2, x^4}, {x, -2, 2}
   , PlotRange -> {-1, 5}
   , PlotStyle -> {Automatic, Red}
   ];
p2 = RegionPlot[reg
   , PlotStyle -> HatchFilling[]
   , BoundaryStyle -> None
   ];
gr = Graphics[{#, Rectangle[]}
     , ImageSize -> Small
     ] & /@ {Red, ColorData[97][1], HatchFilling[]};
legend = SwatchLegend[{Red, ColorData[97][1], None}
   , {x^4, x^2, x^2 < y < x^4}
   , LegendMarkers -> gr
   , LegendMarkerSize -> 20];
Legended[
 Show[p1, p2]
 , Placed[legend, {0.65, 0.8}]
 ]

score 2 · Answer 4 · edited Apr 13 '17 at 12:56

2

I got this here

Plot[{Max[x^2, x^4], x^2, x^4}, {x, -2, 2}, PlotRange -> {-1, 5}, 
PlotStyle -> {Automatic, Red}, Filling -> {1 -> {2}}]

edited Apr 13 '17 at 12:56

Community

1

answered Oct 07 '15 at 06:58

Hubble07

3,614
13
23

just saw the answer by @Lou which I believe is from the same source. – Hubble07 Oct 07 '15 at 07:00

score 1 · Answer 5 · answered Jan 13 '24 at 09:48

Another way is decreasing the MaxRecursion to <=1. We compare with the four cases.( Version 14.0 )

plots = Plot[{x^2, x^4}, {x, -2, 2}, PlotRange -> {-1, 5}, 
     PlotStyle -> {Automatic, Red}, 
     Filling -> {1 -> {{2}, {LightBlue, White}}}, MaxRecursion -> #, 
     PlotLabel -> "MaxRecursion=" <> ToString@#] & /@ {0, 1, 2, 4};
GraphicsGrid[Partition[plots, 2, 2]]

I belive that one of the problem is that y=x^2 and y=x^4 tangent at x=0 so x^2-x^4 does not change the sign at x=0.

Shading a region where an inequality is satisfied

5 Answers5

Update

Linked

Related