how to do VectorPlot?

Question

I have a problem with VectorPlot for spin current density and I tried it my self but not working. Here is the code according to Jens solution:

Clear[x, y, ψ1, ψ2, ψ3, ψ4, eqn, eqnWithInitial,v, j];
eqn = Thread[
   I D[{ψ1[x, y, t], ψ2[x, y, t], ψ3[x, y, t], ψ4[
        x, y, t]}, 
      t] == {v (-I D[ψ3[x, y, t], x] - D[ψ3[x, y, t], y]) + 
      2 Δ ψ4[x, y, t], 
     v (-I D[ψ4[x, y, t], x] - D[ψ4[x, y, t], y]), 
     v (-I D[ψ1[x, y, t], x] + D[ψ1[x, y, t], y]), 
     v (-I D[ψ2[x, y, t], x] + D[ψ2[x, y, t], y]) + 
      2 Δ ψ1[x, y, t]}];
eqnWithInitial = 
  Join[eqn, 
   Thread[{ψ1[x, y, 0], ψ2[x, y, 0], ψ3[x, y, 
       0], ψ4[x, y, 0]} == {1, 1, 1, 
       1} (x + I*y) Exp[-(x^2 + y^2)]], 
   Thread[{ψ1[-5, y, t], ψ2[-5, y, t], ψ3[-5, y, 
       t], ψ4[-5, y, t]} == {ψ1[5, y, t], ψ2[5, y, 
       t], ψ3[5, y, t], ψ4[5, y, t]}], 
   Thread[{ψ1[x, -5, t], ψ2[x, -5, t], ψ3[x, -5, 
       t], ψ4[x, -5, t]} == {ψ1[x, 5, t], ψ2[x, 5, 
       t], ψ3[x, 5, t], ψ4[x, 5, t]}]];

v = 1;

Δ = 1;

tMax = 8;

solution = 
  First@NDSolve[
    eqnWithInitial, {ψ1[x, y, t], ψ2[x, y, t], ψ3[x, y,
       t], ψ4[x, y, t]}, {x, -5, 5}, {y, -5, 5}, {t, 0, tMax}, 
    Method -> {"MethodOfLines", 
      "SpatialDiscretization" -> {"TensorProductGrid", 
        "DifferenceOrder" -> "Pseudospectral"}}];

Ψ1[x_, y_, t_] = ψ1[x, y, t] /. solution;
Ψ2[x_, y_, t_] = ψ2[x, y, t] /. solution;
Ψ3[x_, y_, t_] = ψ3[x, y, t] /. solution;
Ψ4[x_, y_, t_] = ψ4[x, y, t] /. solution;  
pl = Table[
   Plot3D[{Re[Ψ1[x, y, t]] - 2, 
     2 + Re[Ψ2[x, y, t]], Re[Ψ3[x, y, t]] - 1,
      1 + Re[Ψ4[x, y, t]]}, {x, -5, 5}, {y, -5, 5}, 
    PlotRange -> {-3, 3}, 
    PlotStyle -> {Red, Directive[Opacity[.9], Orange]}, 
    BoxRatios -> 1], {t, 0, tMax, tMax/20}];

p2 = Table[
   Plot3D[Abs[Ψ2[x, y, t]], {x, -5, 5}, {y, -5, 5}, 
    PlotRange -> {-3, 3}, 
    PlotStyle -> {Orange, Directive[Opacity[.9]]}, 
    BoxRatios -> 1], {t, 0, tMax, tMax/20}];

Here is the code for the Spin current

j[x_, y_, t_] = -(I/
    2) (Conjugate[Ψ2[x, y, t]]*
      D[Ψ2[x, y, t], {{x, y}}] - 
     D[Conjugate[Ψ2[x, y, t]], {{x, y}}]*Ψ2[x, y, t]);

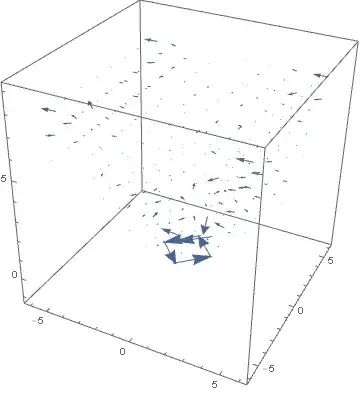
VectorPlot3D[Re[j[x, y, t]], {x, -5, 5}, {y, -5, 5}, {t, 0, tMax}]

Any comments would be greatly appreciated.

Here is with some modification

j[x_, y_,t_] = -(I/2) (Conjugate[\[CapitalPsi]3[x, y, t]]*D[\[CapitalPsi]3[x, y, t], {{x, y}}]-Conjugate[D[\[CapitalPsi]3[x, y, t], {{x, y}}]]*\[CapitalPsi]3[x,y,t]);

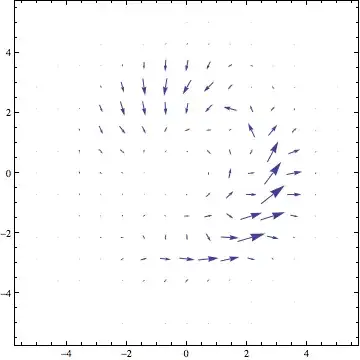
VectorPlot[j[x, y, 3], {x, -5, 5}, {y, -5, 5}]

My follow up question is to plot the z-component for the (rot j[x, y, t]). There is still derivative before Conjugate in the new expression.

vecField[x_, y_, t_]=D[Part[j[x, y, t], 2], x]-D[Part[j[x, y, t], 1], y];
VectorPlot[vecField[x, y, 3], {x, -5, 5}, {y, -5, 5}]

the z component of the current density:

$\nabla\times J=(\frac{\partial J_y}{\partial x}-\frac{\partial J_x}{\partial y})$

Here is my trial but still unable to plot the z component of the current density:

j4a[x_, y_, t_] = 
  Part[-(I/2) (Conjugate[D[\[CapitalPsi]4[x, y, t], y]]*
       D[\[CapitalPsi]4[x, y, t], x, {y, 2}] - 
      Conjugate[D[\[CapitalPsi]4[x, y, t], x, {y, 2}]]*
       D[\[CapitalPsi]4[x, y, t], y]), 2];

j4b[x_, y_, t_] = 
  Part[-(I/2) (Conjugate[D[\[CapitalPsi]4[x, y, t], y]]*
       D[\[CapitalPsi]4[x, y, t], x, {y, 2}] - 
      Conjugate[D[\[CapitalPsi]4[x, y, t], x, {y, 2}]]*
       D[\[CapitalPsi]4[x, y, t], y]), 1];

vecField[x_, y_, t_] = j4a[x, y, t] - j4b[x, y, t];

VectorPlot[vecField[x, y, 3], {x, -5, 5}, {y, -5, 5}]

with an error of

Part::partw: Part 1 of {} does not exist. >>

Here is my own answer after explicitly written the expression for the current density

myrotorz1[x_, y_, 
  t_] = -I/2*(-Conjugate[D[\[CapitalPsi]1[x, y, t], y]]*
     D[\[CapitalPsi]1[x, y, t], x] + 
    D[\[CapitalPsi]1[x, y, t], y]*
     Conjugate[D[\[CapitalPsi]1[x, y, t], x]] + 
    Conjugate[D[\[CapitalPsi]1[x, y, t], x]]*
     D[\[CapitalPsi]1[x, y, t], y] - 
    D[\[CapitalPsi]1[x, y, t], x]*
     Conjugate[D[\[CapitalPsi]1[x, y, t], y]])

Plot3D[Re[myrotorz1[x, y, 0]], {x, -5, 5}, {y, -5, 5}, 
 PlotRange -> All]

A follow up question, I would like to plot myrotorz1[x, y, t] as a function of t but shows an error. Any comments would be highly appreciated

Data = NIntegrate[myrotorz1[x, y, t], {x, -5, 5}, {y, -5, 5}];
Table[Plot[Re[Data], {t, 0, 6, 0.1}], PlotRange -> All]

These are the errors I get

    (Debug) During evaluation of In[5]:= NIntegrate::inumr: The integrand myrotorz1[x,y,t] has evaluated to non-numerical values for all sampling points in the region with boundaries {{-5,5},{-5,5}}. >>

(Debug) During evaluation of In[5]:= NIntegrate::inumr: The integrand myrotorz1[x,y,t] has evaluated to non-numerical values for all sampling points in the region with boundaries {{-5,5},{-5,5}}. >>

(Debug) During evaluation of In[5]:= Table::itform: Argument PlotRange->All at position 2 does not have the correct form for an iterator. >>

(Debug) Out[6]= Table[Plot[Re[Data], {t, 0, 6, 0.1}], PlotRange -> All]

(Debug) During evaluation of In[3]:= General::stop: Further output of NIntegrate::inumr will be suppressed during this calculation. >>

General::stop: Further output of NIntegrate::inumr will be suppressed during this calculation. >>

@rhermans, yeah a 2D vector & would like to plot with VectorPlot. — user34056, Oct 07 '15 at 19:24

score 3 · Answer 1 · edited Apr 13 '17 at 12:55

3

I see two problems,

VectorPlot3D expects a 3D vector, not a 2D.

Length@Re[j[x, y, t]]

2

Your function contains derivatives of the Conjugate function

Re[j[1, 1, 1]]

{(-0.04592782419744598 + 
   Im[(-0.05339043940427357 + 
      0.03730404617998509*I)*
     Derivative[1][Conjugate][
      0.12372410925234094 + 0.1480141706278738*
        I]])/2, (-0.04165285128771159 + 
   Im[(-0.049115484047442155 + 
      0.0376862735996922*I)*
     Derivative[1][Conjugate][
      0.12372410925234094 + 0.1480141706278738*
        I]])/2}

That problem already have somehow unsatisfactory answers here, and here

But if you redefine the function to avoid D[Conjugate[

j[x_, y_,t_] = -(I/2) (Conjugate[Ψ2[x, y, t]]*
      D[Ψ2[x, y, t], {{x, y}}] - 
     Conjugate[D[Ψ2[x, y, t], {{x, y}}]]*Ψ2[x,
        y, t]);

VectorPlot3D[
 Append[Re[j[x, y, t]], 0], {x, -5, 5}, {y, -5, 5}, {t, 0, tMax}]

Mathematica graphics

edited Apr 13 '17 at 12:55

Community

1

answered Oct 07 '15 at 19:17

rhermans

36,518
4
57
149

thank you so much! The problem was with the derivative of the conjugate. It works fine now! Here also with Table: vectors = Table[Re[j[x, y, t]] /. (Derivative[1][Conjugate][x_ /; NumericQ[x]] -> 0), {x, -5, 5, 1}, {y, -5, 5, 1}, {t, 0, tMax, 1}]; ListVectorPlot[vectors] – user34056 Oct 08 '15 at 06:31
I would like to plot the curl of j[x, y, t] in the z direction but couldnt show up: Here is the code: vecField[x_, y_, t_] = D[j[x, y, t], {x}] - D[j[x, y, t], {y}]; VectorPlot3D[ Append[Re[vecField[x, y, t]], 0], {x, -5, 5}, {y, -5, 5}, {t, 0, tMax}] – user34056 Oct 09 '15 at 10:07
Please look at the output of your functions BEFORE you try to plot them. The code you give also has he same problem of including D[Conjugate[ – rhermans Oct 09 '15 at 10:50
the main problem is on how to over come the extra D[Conjugate[ in the code: vecField[x_, y_, t_] = D[Part[j[x, y, t], 2], x] - D[Part[j[x, y, t], 1], y]; – user34056 Oct 09 '15 at 18:26

how to do VectorPlot?

1 Answers1