How do I make a log plot where the plot is logarithmic in the distance from the X-Axis (including negative values)?

Question

For example, if I were to do a plot of Sin[x], I would get what looks like a Log plot of Sin[x], with another log plot of -Sin[x] that has been flipped upside down and placed underneath the first one, in this way, the plot is logarithmic in distance from the x-axis, and can show both positive and negative values.

Answer 1

I interpret this question quite differently from the other responders.

I would get what looks like a Log plot of Sin[x], with another log plot of -Sin[x] that has been flipped upside down and placed underneath the first one.

We can do that rather literally like this:

p1 = LogPlot[Sin[x], {x, 0, 15}];
p2 = LogPlot[-Sin[x], {x, 0, 15}];

pivot = Last[AxesOrigin /. Options[p2]];

Show[
 p1,
 MapAt[Scale[#, {1, -1}, {0, pivot}] &, p2, 1],
 PlotRange -> All
]

This is not an ideal method however and I shall be working on a better one.

---

Here is a second method based on manipulating the output of LogPlot. If the logarithmic ticks are not required this is overly complicated. The Red/Blue style is added only for illustration.

p = LogPlot[{Sin[x], -Sin[x]}, {x, 0, 15}, PlotStyle -> {Red, Blue}];

pivot = Last[AxesOrigin /. Options@p];

MapAt[# /. Line[x__] :> Line[{#, 2 pivot - #2} & @@@ x] &, p, {1, 1, 4}] /. {
  (Ticks -> {xdat_, ydat_}) :>
   Ticks -> {xdat, Join[ydat, {2 pivot - #, ##2} & @@@ ydat]},
  (PlotRange -> {x_, {y_, Y_}}) :> PlotRange -> {x, {2 y, Y}}
 }

---

If $y$ ticks are unimportant you might use something like this:

logify[off_][x_?Positive] := Max[0, (off + Re@Log@x)/off]
logify[off_][x_?Negative] := Min[0, (off + Re@Log@x)/-off]

The parameter off is a scaling function. Example of use:

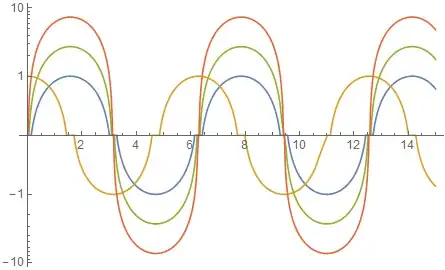
Plot[
 logify[1] /@ {Sin@x, Cos@x, E Sin[x], E^2 Sin[x]},
 {x, 0, 15},
 Axes -> {True, False},
 Evaluated -> True
]

As above but with logify[5]:

Update

I am four years overdue on this, but now with ticks by leveraging ScalingFunctions, which unofficially works in Plot in Mathematica 10 but may not in earlier editions.

logify[off_][a_List] := logify[off] /@ a
logify[off_][x_?Positive] := Max[0, (off + Re@Log@x)/off]
logify[off_][x_?Negative] := Min[0, (off + Re@Log@x)/-off]

invlog[off_][a_List] := invlog[off] /@ a
invlog[off_][x_?Positive] :=  Exp[ x*off - off]
invlog[off_][x_?Negative] := -Exp[-x*off - off]

Application:

Plot[
 {Sin@x, Cos@x, E Sin[x], E^2 Sin[x]}, {x, 0, 15},
 ScalingFunctions -> {logify[2], invlog[2]}
]

Answer 2

Plot[{Sin@x, Sign@Sin@x Log@Abs@Sin@x}, {x, 0, 10 Pi}, Exclusions -> {(Sin@x == 0)}]

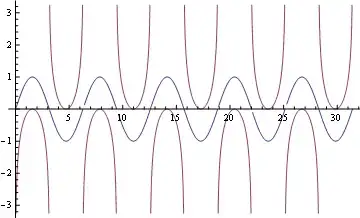
Edit

Just a nice plot with Log@Sin@x

Framed@Plot[{Sign@Sin@x Log@Abs@Sin@x, Log@Tan[x + Pi], -Log@Tan[x - Pi/2]}, {x, 0, Pi}, 
  Exclusions -> {(Sin@x == 0)}, PlotRange -> {Automatic, {-5, 5}}, 
  Filling -> {1 -> {3}, 1 -> {2}}, 
  PlotStyle -> {{Thick, Blue}, {Thick, Red}, {Thick, Red}}, 
  AxesStyle -> Directive[Gray, 12]]

Answer 3

Something like :

f[x_] := Which[Sin[x] > 0, Log[Sin[x]], Sin[x] < 0, -Log[-Sin[x]]]