I am solving differential equation of second order
g = 9.81
k = 0.009
r = 10
b = 0
ω = Sqrt[g/r]
s = NDSolve[{r/g*y''[x] + (k*r/g + b*r^2/mg)*y'[x]^2 + Cos[x] - k*Sin[x] == 0,
y[0] == π/2, y'[0] == ω, y, {x, 0, 2}]
and I know hot to display the result.
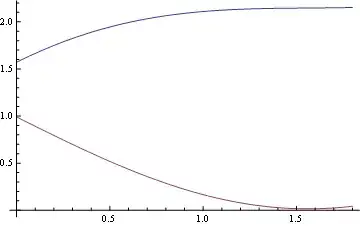
Plot[Evaluate[y[x] /. s], {x, 0, 1.8}, PlotRange -> All]
Plot[Evaluate[y'[x] /. s], {x, 0, 1.8}, PlotRange -> All]
But I do not know how to display y' as function of y, i.e. y'[y].
I would also like to know how to find the value of x for y=-\[Pi]/2.
Is this possible?
Thanks for help



mgnotm*g. InterestingNDSolvegives nor error message. What do I overlook? – Oct 13 '15 at 19:17