I would need to identify the types of regular polygons forming the surface of a convex hull of 3D points. If I e.g. take the following example of a regular polyhedron
ConvexHullMesh[N[PolyhedronData["Dodecahedron", "VertexCoordinates"]]]
The convex hull routine returns a triangulated mesh surface. Is there any simple way to convince Mathematica to return the surface as polyhedrons (in this case pentagons) instead of a triangulation.
To illustrate the issue further, e.g if one applies
MeshCells[ConvexHullMesh[N[PolyhedronData["Dodecahedron", "VertexCoordinates"]]], 2]
Mathematica only returns triangles.
If one applies
ConvexHullMesh[N[PolyhedronData["Dodecahedron", "VertexCoordinates"]]] // FullForm
There is the option "CoplanarityTolerance". But I do not know how to use it.
Any ideas?
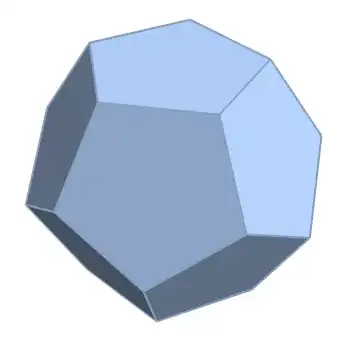
![dodecahedron as a MeshRegion[]](../../images/c43a7a1903223fbad85db4603865b465.webp)



Method, and it's forBoundaryMeshRegion, not forConvexHullorBoundaryMesh... – Szabolcs Oct 14 '15 at 15:46