Plot $\arg(z)$ in an Argand diagram and display the angle

Question

I'd like to ask you about the way to show the $\arg(z)$ annotation about the angle. My point is to show $\frac{2\pi}{3}$ and $\frac{5\pi}{6}$ on the image.

What I mean:

_{(source: brocku.ca)}

Is there any way to achieve similar effect in Mathematica?

My code:

    Show[%6, Axes -> True, Method -> {"ScRegionPlot[
      Pi/4. <= Arg[x + I y] <= Pi, {x, -1, 1}, {y, -.1, 1}, 
      GridLines -> {{-.15}, {0}}, 
      PlotPoints -> 60, Show[%6,Axes\[Rule]True,Method\[Rule]{" \
ScRegionPlot[
       Norm[x + I y + .15] < 0.6 && 
       Pi/4. <= Arg[x + I y] <= Pi, {x, -1, 1}, {y, -.1, 1}, 
       AspectRatio -> 
       Automatic] alingFunctions "\[Rule]None," \
TransparentPolygonMesh "\[Rule]True}]
      AspectRatio -> Automatic]alingFunctions" -> None, 
   "TransparentPolygonMesh" -> True}]

Graphics[Disk[{0, 0}, 1, {2 π/3, 5 π/6}], Axes -> True]? — J. M.'s missing motivation, Oct 17 '15 at 13:58
Thank you but I wanted to print the angle on the image. Both of them. Another example: http://www.physics.brocku.ca/PPLATO/h-flap/math3_3f_2.png — Pawel Gumiela, Oct 17 '15 at 14:00
Try adding Text[#, {Cos[#], Sin[#]}, {1, -1}] & /@ {2 π/3, 5 π/6} — J. M.'s missing motivation, Oct 17 '15 at 14:04

score 7 · Accepted Answer · answered Oct 17 '15 at 19:47

roots = z /. Solve[z^3 == 1, z];
pts = {Re[#], Im[#]} & /@ roots;
args = Arg /@ Cases[roots, _?(Im[N[#]] != 0 &)];

Module[{pr = 1.25, radius = {1/4, 3/8}},
 Graphics[{
   Thick,
   Arrow[{{-pr, 0}, {pr, 0}}],
   Arrow[{{0, -pr}, {0, pr}}],
   Text[Style[Subscript[z, 0], 18, Bold],
    pts[[1]], {0, -2}],
   Text[Style[Subscript[z, 1], 18, Bold],
    pts[[3]], {0, -2}],
   Text[Style[Subscript[z, 2], 18, Bold],
    pts[[2]], {0, 2}],
   {
      Circle[{0, 0}, #[[1]], {0, #[[2]]}],
      Text[Style[#[[2]], 14, Bold], #[[1]]*
        Through[{Cos, Sin}[#[[2]]/2]],
       {-1.25, -Sign[#[[2]]]}]} & /@
    Transpose[{radius, args}],
   AbsolutePointSize[10],
   Point[pts],
   AbsoluteDashing[{10, 10}],
   Line[{{0, 0}, #}] & /@ pts},
  Axes -> True,
  Ticks -> {Range[-1, 1, 1/2], Range[-1, 1, 1]},
  TicksStyle -> Directive["Label", 14],
  PlotRange -> {{-pr, pr}, {-pr, pr}},
  AxesLabel -> (Style[#, 14, Bold] & /@ {Re, Im})]]

murray · Answer 2 · 2015-10-18T16:01:50.420

A question on plotting complex numbers begs for an answer that directly uses complex numbers rather than requires pulling the complex numbers apart into real and imaginary parts. Such an answer is allowed by David Park's Presentations( add-on (https://home.comcast.net/~djmpark/DrawGraphicsPage.html):

   <<Presentations`

   roots = z /. Solve[z^3 == 1, z];
   args = Arg /@ Select[roots, ! Element[#, Reals] &];

   With[{rng = 1.25, radii = {1/4, 3/8}, arcOffset = 1.4},
     Draw2D[{
       Thick,
       (*arrow axes *)
       ComplexArrow[{-rng, rng}], ComplexArrow[{-rng I, rng I}],

       (* labeled arcs *)
       ComplexCircle[0, First@#, {0, Last@#}] & /@ 
       Transpose[{radii, args}],
       ComplexText[Last@#, 
       ComplexPolar[ arcOffset First@#, Last@#/2], {-1, 0}] & /@ 
       Transpose[{radii, args}],

       (* lines to roots *)
       Dashing[0.035], 
       ComplexLine[{0, #}] & /@ Rest@roots,

      (* labeled roots *)
      PointSize[0.025], ComplexPoint /@ roots,
      ComplexText[Sequence @@ #] & /@ 
        Transpose[{Style[#, 18] & /@ {Subscript[z, 0], Subscript[z, 2],Subscript[z, 1]}, 
          roots, {{0, -2}, {0, 2}, {0, -2}}}]
     },
     PlotRange -> rng,
     Axes -> True, AxesLabel -> {Re, Im},
     Ticks -> {Range[-1, 1, 1/2], Range[-1, 1, 1]},
     TicksStyle -> Directive["Label", 14, FontWeight -> "Medium"],
     BaseStyle -> Directive[14, Bold]
   ]
  ]

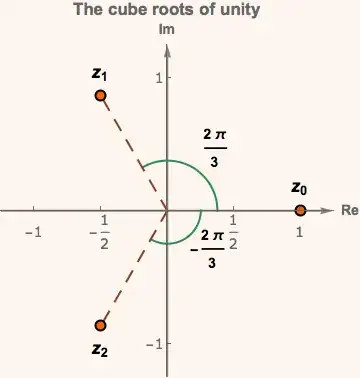
Here's the same thing decorated a bit with use of color, etc.:

   With[{rng = 1.25, radii = {1/4, 3/8}, arcOffset = 1.4},
     Draw2D[{
       Thick,
       (*arrow axes *)
       {Gray, ComplexArrow[{-rng, rng}], ComplexArrow[{-rng I, rng I}]},

       (* labeled arcs *)
       {Legacy@SeaGreen, ComplexCircle[0, First@#, {0, Last@#}] & /@ 
         Transpose[{radii, args}]},
       ComplexText[Last@#, 
       ComplexPolar[ arcOffset First@#, Last@#/2], {-1, 0}] & /@ 
       Transpose[{radii, args}],

       (* lines to roots *)
       {Dashing[0.035], Legacy@BrownOchre,
       ComplexLine[{0, #}] & /@ Rest@roots},

      (* labeled roots *)
      ComplexCirclePoint[#, 5, Black, Legacy@CadmiumOrange] & /@ roots,
      ComplexText[Sequence @@ #] & /@ 
        Transpose[{Style[#, 18] & /@ {Subscript[z, 0], Subscript[z, 2],Subscript[z, 1]}, 
          roots, {{0, -2}, {0, 2}, {0, -2}}}]
     },
     PlotRange -> rng,
     Axes -> True, AxesLabel -> {Re, Im},
     Ticks -> {Range[-1, 1, 1/2], Range[-1, 1, 1]},
     TicksStyle -> Directive["Label", 14, FontWeight -> "Medium"],
     BaseStyle -> Directive[14, Bold],
     Background -> Lighter@Legacy@Linen,
     PlotLabel -> "The cube roots of unity"
   ]
  ]

Plot $\arg(z)$ in an Argand diagram and display the angle

2 Answers2

Linked