Huge overhead in RandomPoint[ImplicitRegion]

Question

Commenting answers of this question @JasonB noticed the big overhead of RandomPoint

region = ImplicitRegion[1 > 1/(2 q) > p > 1/2, {p, q}];
First@RepeatedTiming[RandomPoint[region], 1]

0.1010

Compare with

First@RepeatedTiming[RandomPoint[Disk[]], 1]

0.00019

Further test for more points ( Mma 10.3 Win7 64 ):

tl = Table[
  {
   2^k,
   First@RepeatedTiming[RandomPoint[region, 2^k], 1]
   }, {k, 24}]

Plot

ListLogLogPlot[
 tl
 , PlotTheme -> "Detailed"
 , FrameLabel -> {"# of Random Points", "RepeatedTiming"}]

Its 0.1 seconds overhead which seems unreasonable and we suspect a bug.

Q: Can we find the source of the overhead and a reasonable workaround?

EDIT

tl2 = Table[
  {
   2^k,
   First@RepeatedTiming[RandomPoint[Disk[], 2^k], 1]
   }, {k, 25}]

ListLogLogPlot[
 {tl, tl2}
 , Joined -> True
 , PlotTheme -> "Detailed"
 , FrameLabel -> {"Number of Random Points", "RepeatedTiming"}
 , PlotLegends -> {"ImplicitRegion", "Disk"}]

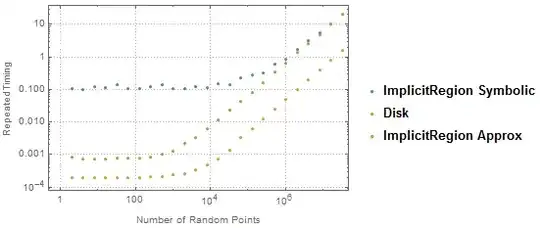
When you read the label on the first axis as "Slot of Random Points" :p — Marius Ladegård Meyer, Oct 20 '15 at 13:41
Somehow I wouldn't expect a low overhead here ... ImplicitRegion is a symbolic region. There must be a lot of symbolic processing going on at the beginning: Is the region bounded? Based on its shape, what method is likely to be fastest for large numbers of points? Then transform the region into the proper form for the method (e.g. is it a rejection method, or direct sampling?) Disk is a predefined region so RandomPoint can easily specialize for it. It probably has a a RandomPointInDisk internal generator for it... But that's not going to work for an implicit region. — Szabolcs, Oct 20 '15 at 14:13
Or am I missing something? How would you implemented RandomPoint for general implicit regions? BTW thank you for showing me RepeatedTiming! I was still using my own custom version. — Szabolcs, Oct 20 '15 at 14:14

score 6 · Accepted Answer · answered Oct 20 '15 at 15:17

As suggested by @Szabolcs, "a lot of symbolic processing" is behind when using symbolic representation. Numerical approximation severely reduces the overhead.

reg = ImplicitRegion[
  Evaluate[
   N@Reduce[1 > 1/(2 q) > p > 1/2]
   ], {p, q}]

ImplicitRegion[0.5 < q < 1. && 0.5 < p < 0.5/q, {p, q}]

First@RepeatedTiming[RandomPoint@reg, 1]

0.000687

tl3 = Table[
   {
    2^k,
    First@RepeatedTiming[RandomPoint[reg, 2^k], 1]
    }, {k, 25}];

Plot

ListLogLogPlot[
 {tl, tl2, tl3}
 , Joined -> False
 , PlotTheme -> "Detailed"
 , FrameLabel -> {"Number of Random Points", "RepeatedTiming"}
 , PlotLegends -> {"ImplicitRegion Symbolic", "Disk", 
   "ImplicitRegion Approx"}]

Huge overhead in RandomPoint[ImplicitRegion]

1 Answers1

Linked