A method to draw a surface around a set of regularly spaced points

Question

This is mostly an artistic endeavour.

I have a 3D array of points, 1 representing a point within the surface, -1 without. The shape is not convex. I would like to produce a surface which encloses the points. One simple way is ListContourPlot:

The surface is not very pleasing though; it is similar to the result of simply building the shape out of cubes without using any interpolation. Perhaps as a result of this, it is also very large, taking up 2gb of RAM.

What is a better way of doing this?

Here is a subset of my data in .MAT format.

Answer 1

So the algorithm in the paper I linked to in a comment, "Surface Extraction from Binary Volumes with Higher-Order Smoothness" by Lempitsky (2010), turned out to be pretty easy to implement (though for speed I changed eq. (10a) to a difference of Gaussians). And it works much better than my attempt, so I'm replacing that with this.

Build a signed distance field (SDF):

dOut = ImageClip[
   ImageSubtract[DistanceTransform[Image3D[-data]], 0.5], {0, 1*^6}];
dIn = ImageClip[
   ImageSubtract[DistanceTransform[Image3D[data]], 0.5], {0, 1*^6}];
sdf = ImageSubtract[dOut, dIn];

Define lower and upper bounds for the smoothed SDF:

l = ImageApply[Which[# >= 0, Max[# - 1, 0], True, -1*^6] &, sdf];
u = ImageApply[Which[# <= 0, Min[# + 1, 0], True, 1*^6] &, sdf];

Define the filtering operation:

filter[r_][sdf_] := 
 ImageApply[
  Clip[#1, {#2, #3}] &, {ImageSubtract[
    ImageMultiply[GaussianFilter[sdf, r], 4/3], 
    ImageMultiply[GaussianFilter[sdf, 2 r], 1/3]], l, u}]

And that's it!

If you don't have much time, use a large radius and a handful of iterations. Otherwise, use a small radius and a large number of iterations for higher-quality results.

draw[sdf_] := 
 ListContourPlot3D[ImageData[sdf], Contours -> {0}, 
  ContourStyle -> White, Mesh -> None]
draw[sdf]
Print[draw[filter[4][sdf]]]; // Timing
Print[draw[Nest[filter[2], sdf, 10]]]; // Timing
Print[draw[Nest[filter[1.2], sdf, 100]]]; // Timing

(* {6.74007, Null} *)

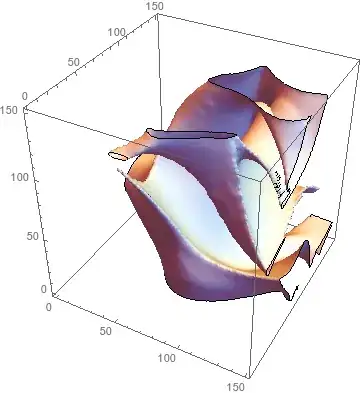
(* {39.5372, Null} *)

(* {365.001, Null} *)