0

I'm not getting the expected output when I use Collect with indexed variables.

mA = Array[a[##] &, {2, 2}]
Collect[CharacteristicPolynomial[mA, t], t]

produces 

{{a[1, 1], a[1, 2]}, {a[2, 1], a[2, 2]}}
t^2 - a[1, 2] a[2, 1] + t (-a[1, 1] - a[2, 2]) + a[1, 1] a[2, 2]

Note that although I've tried to collect terms in t, constant terms have not been collected. Explanation?

Mma has a standard order when it collects powers. This order is not being honored. It is also standard for Mma to collect terms in t^0 (since I am collecting in t in this example). This also is not being honored. I realize the coefficients in this example are not symbols. My question is simple: why should this matter when I am collecting in t?

Contrast with this second example, which does give the expected output:

mA = {{a11, a12}, {a21, a22}}
Collect[CharacteristicPolynomial[mA, t], t]

produces

{{a11, a12}, {a21, a22}}
-a12 a21 + a11 a22 + (-a11 - a22) t + t^2

Note the standard ordering in the variable t in the second example.

Alan
  • 13,686
  • 19
  • 38
  • 1
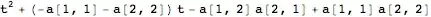
    It does : Collect[CharacteristicPolynomial[mA, t], t, h] – Dr. belisarius Oct 23 '15 at 16:48
  • What would be your expected output? – MarcoB Oct 23 '15 at 17:28
  • @MarcoB I've edited the question to be clear about the expected output. I think belisarius may be suggesting my expectation is wrong, but I need more of a hint. Thanks. – Alan Oct 23 '15 at 22:02
  • In your last example you show the standard ordering of the variables you want to see. But Mathematica doesn't see expressions of the form a[i_, j_] as variables because they are not atoms. So standard ordering of variables does not apply. – m_goldberg Oct 23 '15 at 22:53
  • @m_goldberg But ... I'm asking to collect in t. So why does that matter? (Clearly it does, but I'm missing something.) – Alan Oct 23 '15 at 22:55
  • You got collection over powers of t. What you are complaining about is how t-free terms are ordered. All I can say is that a[1, 2] looks very different than a12 to Mathematica. Use FullForm to examine the results of your to examples of collecting terms to see how different the internal forms are. – m_goldberg Oct 23 '15 at 23:21
  • @m_goldberg Mma has a standard order when it collects powers. This order is not being honored. It is also standard for Mma to collect terms in t^0 (in this example). This also is not being honored. Sure I realized the coefficients are not symbols. My question is simple: why should this matter when I am collecting in t? – Alan Oct 24 '15 at 17:36
  • Note that directly entering -a[1, 2] a[2, 1] + a[1, 1] a[2, 2] + t (-a[1, 1] - a[2, 2]) + t^2 will give you the scrambled-looking output you have. Consider this: SetAttributes[f, Orderless]; f @@ {-a[1, 2] a[2, 1], a[1, 1] a[2, 2], t (-a[1, 1] - a[2, 2]), t^2}. – J. M.'s missing motivation Oct 24 '15 at 17:55
  • Try this: cp = CharacteristicPolynomial[mA, t] Collect[cp - (cp /. t -> 0), {t, t^2}] + (Evaluate[(cp /. t -> 0)] // HoldForm) . Have fun! – Alexei Boulbitch Oct 24 '15 at 18:04

1 Answers1

2

I can think of a couple of ways to interpret this question.

If the problem is getting the coefficients, use CoefficientList or CoefficientArrays:

mA = Array[a[##] &, {2, 2}];
CoefficientList[CharacteristicPolynomial[mA, t], t]
(*  {-a[1, 2] a[2, 1] + a[1, 1] a[2, 2], -a[1, 1] - a[2, 2], 1}  *)

If that's not right, maybe it's output formatting.

PolynomialForm[Collect[CharacteristicPolynomial[mA, t], t], 
 TraditionalOrder -> True]

Mathematica graphics

See for instance, How to put terms in lexicographic order?, and its linked questions.

Community
  • 1
Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • Your second suggestion is interesting and somewhat helpful. Your first just however just underlines my question: as I said: I just want to understand why terms in t^0 are not collected together by Collect. I thought that was what Collect was supposed to do. How am I misreading the documentation? – Alan Oct 25 '15 at 16:38
  • @Alan I suppose it is because Plus is Flat and does not support grouping in the way it is done in school algebra. – Michael E2 Oct 25 '15 at 18:35
  • Aha, now that is a good answer! I am going to accept your answer but it would be best if you could move your comment to the answer. An implication of this is that when the documentation says that Collect "collects together terms involving the same powers of objects matching x" that this does not mean it will collect together terms in x^0. Thanks. – Alan Oct 25 '15 at 21:15