solve tricky nonlinear ODE on a grid

Question

I've been working on the same question for a while now and would appreciate any advice on what I'm doing wrong or any direction on how to actually solve the problem. :) On xzczd's advice, I retried with just using NDSolve. Also on xzczd's advice, I simplified the problem so that it is copy-paste-runnable.

Here's explicit code of what I'm doing.

(* Parameters *)
α = 4/100; γ = 2; ψ = 2; A = 1/10; θ = 10; δ = 0; σ = 1/10;

(* Define a function *)
ϕ[i_] := i - θ/2 i^2 - δ;

(* Boundaries *)
b = Rationalize[0.11619,10^-10]; (* Rationalize common-valued boundary point s*)

(* Some functions for ODE and solution to i *)
l1 = (1 - z) (1 - z y'[z]/y[z]);
l2 = z (1 + (1 - z) y'[z]/y[z]);
m = z^2 (1 - z)^2 y''[z]/y[z];

(* Solve for i as a function of y and y' *)
isolve = FullSimplify[Solve[{
 (((A - i1) (1 - z) + (A - i2) z)/y[z])^(1/ψ) == α/(ϕ'[i1] (y[z] - z y'[z])),
 (((A - i1) (1 - z) + (A - i2) z)/y[z])^(1/ψ) == α/(ϕ'[i2] (y[z] + (1 - z) y'[z]))}, {i1, i2}]];

(* There are three potential solutions here.  Only the first is
correct, I believe *)
Dimensions[isolve]
i1star = i1 /. isolve[[1, 1]]; 
i2star = i2 /. isolve[[1, 2]];
cstar = (A - i1star) (1 - z) + (A - i2star) z;

(* Simplify ODE *)
ode = Simplify[ ( α/(1 - 1/ψ) ((cstar/y[z])^(1 - 1/ψ) - 1) + ϕ[i1star] l1 + ϕ[i2star] l2 - γ /
    2 (σ^2 l1^2 + σ^2 l2^2) + (σ^2 + σ^2)m/2) ] == 0;

(* Attempt at solution with NDSolve *)
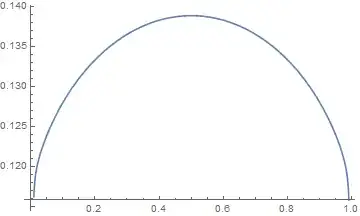
sol = NDSolve[{ode, y[1/100] == b, y[99/100] == b}, y, {z, 1/100, 99/100}, Method -> {"Shooting", "StartingInitialConditions" -> {y[1/100] == b, 
  y'[1/100] == Rationalize[0.1536914, 10^-10]}}, WorkingPrecision -> 30]

As you can see, I'm starting to shoot from within the boundary, to sidestep the end-point singularities. The solution, I know, looks effectively (negative) quadratic, with endpoints at the boundaries. I was previously implementing a finite difference method because it seemed to deal with the end-points singularities better (I only solved on the interior of the grid). It also seemed to solve quickly.

My question is: is there a better, more robust way to solve this than shooting? Or is the math what it is and that's that?

Thank you.

Well, you'd better add a specific working example rather than describe the problem in such an abstract way, or it's hard to give advice. With the information you've mentioned so far, I'll guess that the trouble might lie in FindRoot because solving a large nonlinear system with it can be troublesome and a good starting point is very important for FindRoot to give a proper answer. BTW, just to make sure, you need to solve the ODE yourself rather than using NDSolve, right? — xzczd, Oct 28 '15 at 05:07
Hi xzczd. Thanks for your reply. I was hoping someone like you was going to respond. I've read a lot of your online help about solving ODEs with NDSolve. I tried--A LOT-- with just NDSolve, but I found the shooting method to be unreliable in solving. I believe the problem is that the ODE is singular at both boundary points. By doing differencing myself, I was able to solve a simpler version of the problem and the differencing seemed to be much more robust. I'm still learning. — Jane Doe, Oct 28 '15 at 19:05
There's a typo in the definition of bi and I can't figure out how to fix it. And… currently your big code sample is a little frustrating, it'll be better if you can simplify the code sample a little, for example, the code calculating bi and b and ode isn't relevant, you can just give the result in the sample. If you're not sure whether your deductions for them are correct or not so want us to have a check (it's deprecated, of course), at least add a description for the original problem, I mean, you can express the problem with some equations (in traditional mathematical form). — xzczd, Oct 29 '15 at 02:34
This sounds like a related Q&A: http://mathematica.stackexchange.com/questions/91854/nonlinear-differential-equation-numerical-solution/97733#97733 — Michael E2, Oct 29 '15 at 14:23
@MichaelE2 Actually yesterday I tried to use the method you mentioned in the answer to solve OP's problem but failed 囧, seems that OP's case is more complicated. (Maybe I haven't fully understand your answer.) — xzczd, Oct 30 '15 at 02:36
@xzczd It certainly looks complicated, but in part that's because it's not copy-pasteable. I don't have time to fix it up right now & explore. I think Jane Doe would be more likely to get help if the syntax errors were cleaned up. — Michael E2, Oct 30 '15 at 02:42
Hi xzczd, MichaelE2. Thanks for your feedback and sorry for the previous comment. I've been traveling and unable to address your comments until now. I simplified the code so that it should be copy-paste-runnable in MMA v10.3. The simplification basically involved just entering the value of the boundary rather than calculating it. I don't think it is fruitful to simplify any other part of the code. Feel free to disagree. I'm still learning. — Jane Doe, Nov 01 '15 at 01:10
I agree that the link you posted, MichaelE2, is related to my problem. Thanks. I'll take a look and learn from it. — Jane Doe, Nov 01 '15 at 02:12
Well, you need to add a at in front of our names i.e. write something like @MichaelE2 in your comment, or we won't receive the reminder. (BTW, you can remind only one non-author person commenting/editing the question/answer in a comment.) Then, does the code sample work in v10 or it's just a ineffectual trial? In v9 it fails, at least with the current initial guess. — xzczd, Nov 03 '15 at 03:30
@xzczd It's an ineffectual trial. I'm stuck. I looked at Michael's link and started working through the shooting solution but still haven't gotten anywhere. My problem is a lot messier than the one in the link. I'm sorry that I'm not being clear enough. I'm even learning how to operate Stack Exchange — Jane Doe, Nov 03 '15 at 15:50
@xzczd Don't worry about this example. I've given up. It's too hard for me. Thanks for your help. — Jane Doe, Nov 03 '15 at 22:04

bbgodfrey · Answer 1 · 2017-06-14T21:00:15.610

This computation is failing, because

(-((y[z] (y[z] + (1 - 2 z) y'[z])^2 (y[z] - z y'[z]))/(y[z] - (-1 + z) y'[z])^2))^(1/3)

is complex for typical initial conditions given in the question. Evidently, the wrong branch of cube root has been chosen. Instead, use Surd to assure that the real root is chosen (if it exists). To do so, modify the original ODE in the question as shown.

pode = ode /. Power[x__, 1/3] -> Surd[x, 3] /. Power[x__, 2/3] -> Surd[x, 3]^2 
    /. Power[x__, -1/3] -> 1/Surd[x, 3]
(* 1/100 (-8 + 4/5 2^(2/3) Sqrt[Surd[(y[z] (y[z] + (1 - 2 z) y'[z])^2 (y[z] - 
   z y'[z]))/(y[z] - (-1 + z) y'[z])^2, 3]/(y[z] (y[z] - z y'[z]))] - ...) *)

(The entire expression is quite long.) Then, after a bit of experimentation, the ODE with its boundary conditions can be solved by

sol = NDSolve[{pode, y[1/100] == b, y[99/100] == b}, {y, y'}, {z, 1/100, 99/100}, 
    Method -> {"Shooting", "StartingInitialConditions" -> {y'[1/100] == .94777}}];
Plot[(y[z] /. sol), {z, 0.01, .99}, PlotRange -> All]

For completeness, the value y'[1/100] obtained by NDSolve is

(y'[z] /. sol) /. z -> .01
(* {0.947771} *)

It appears that a very good initial guess is needed, because the solution is near a separatrix of the ODE. The solution can be obtained in a more automated manner using approaches such as those given here.

solve tricky nonlinear ODE on a grid

1 Answers1