Recursive piecewise integral relation with piecewise base case?

Question

How is this recursive formula

$$ f_{n+1}(z) = \int_0^1 f_{n}(z-y)\,{\rm d}y $$

implemented in Mathematica? The base case is

$$ f_1(z) = \begin{cases} 1 & 0\leq z\leq 1 \\ 0 & \text{otherwise} \end{cases} $$

I have tried setting up a recursive integral relation, but my syntax must not be right.

@Pillsy $$f_{X+Y}(z) = \int_{0}^1 f_X(z-y),{\rm d}y = \cases{z&$0 \le z\le 1$\cr 2-z&$1 \le z\leq 2$\cr 0& otherwise}$$
$$f_{X+Y+Z}(z) = \int_{0}^1 f_{X+Y}(z-y),{\rm d}y = \cases{ \frac{z^2}{2}&$0 \le z\le 1$\cr -\frac 3 2- {z}^{2}+3,z&$1 \le z\le 2$\cr \frac 92-3,z+\frac{z^2}{2}&$2 \le z\leq 3$\cr 0& otherwise}$$ — martin, Nov 03 '15 at 21:42
f[1] = Integrate[ PDF[UniformDistribution[{0, 1}], z - y], {y, 0, 1}] /. z -> y; f[n_] := Integrate[f[n - 1] /. y -> z - y, {y, 0, 1}] /. z -> y; f[3] // Simplify ? — Dr. belisarius, Nov 03 '15 at 21:50

score 8 · Answer 1 · edited Apr 13 '17 at 12:55

8

Adapting once again Leonid's solution from here,

f[1, z_] := UnitBox[z - 1/2];
f[n_Integer, z_] := Module[{zl, t},
                           Set @@ Hold[f[n, zl_], 
                           Simplify[Convolve[UnitBox[t - 1/2], f[n - 1, t], t, zl]]];
                           f[n, z]];

f[4, z]

$\displaystyle\begin{cases} -\frac16(-4+z)^3&3\le z<4\\ \frac{z^3}{6}&0<z\le1\\ \frac23-2z+2z^2-\frac{z^3}{2}&1<z\le2\\ -\frac{22}{3}+10z-4z^2+\frac{z^3}{2}&2<z<3\\ 0&\mathtt{True} \end{cases}$

Plot[f[6, t], {t, -2, 2}]

plot of the function

Now, here's the surprise: there's an even shorter implementation for f[]!

f[n_Integer, z_] := BSplineBasis[n - 1, z/n]

edited Apr 13 '17 at 12:55

Community

1

answered Nov 03 '15 at 23:10

J. M.'s missing motivation

124,525
11
401
574

I believe that your final observation can be derived quickly in Fourier space. – bbgodfrey Nov 04 '15 at 14:03
That's correct; in fact, one of the ways to present the theory of B-splines is to consider them as repeated convolutions of a boxcar function. – J. M.'s missing motivation Nov 04 '15 at 14:04

score 6 · Accepted Answer · answered Nov 03 '15 at 22:02

6

f[1] = Integrate[PDF[UniformDistribution[{0, 1}], z - y], {y, 0, 1}] /. z -> y;
f[n_] := f[n] = Integrate[f[n - 1] /. y -> z - y, {y, 0, 1}] /. z -> y // Simplify;
f[3]

Mathematica graphics

answered Nov 03 '15 at 22:02

Dr. belisarius

115,881
13
203
453

score 2 · Answer 3 · edited Apr 13 '17 at 12:19

@Winther's solution is particularly fast from here

adapted slightly:

pwf[z_] := Piecewise[{z[[#]], # - 1 <= y < #} & /@ Range@Length@z]
iidf[n_] := With[{nn = n}, ffunc = Table[If[i == 1, 1, 0], {i, 1, n}]; 
Do[temp = ffunc; temp[[1]] = Integrate[ffunc[[1]], {z, 0, z}];
Do[temp[[k]] = Integrate[ffunc[[k - 1]], {z, z - 1, k - 1}] + 
Integrate[ffunc[[k]], {z, k - 1, z}];, {k, 2, Floor[(i + 1)/2]}];
Do[temp[[k]] = temp[[i - k + 1]] /. z -> i - z;, 
{k, Floor[(i + 1)/2] + 1, i}]; ffunc = temp;, {i, 2, n}];
pwf@ExpandAll[ffunc] /. z -> y]

Plot[Evaluate[iidf@6], {y, 0, 6}, PlotPoints -> 400]

score 2 · Answer 4 · answered Nov 04 '15 at 22:05

Along with @J.M.'s superfast solution, and this nice little identity, where for $X_j \text{ iid},$ uniformly distributed on $[0,1],$

$$\dfrac{1}{n!} \left\langle n \atop k \right\rangle = P\left(\sum_{j=1}^{n}X_j\in[k,k+1]\right)$$

we can get eg eulplot[6, 2], eulplot[12, 5]:

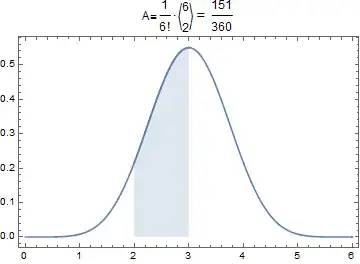
eulerian[k_, n_] := 
CoefficientList[(1 - x)^(n + 1) PolyLog[-n, x]/x, x][[k + 1]]

iid[k_, n_] := eulerian[k, n]/n!

eulplot[n_, pt_] := With[{aa = Piecewise[SortBy[(BSplineBasis[n - 1, 
x/(n)] // PiecewiseExpand)[[1]], Last@# &]]}, 
Show[Plot[Evaluate[aa], {x, 0, n}, PlotPoints -> 1000], 
Plot[Evaluate[aa[[1, pt + 1]]], {x, pt, pt + 1}, Filling -> Axis, 
PlotRange -> {{0, Automatic}, {0, Automatic}}], Frame -> True, 
LabelStyle -> Black, PlotLabel -> StringJoin["A=", ToString[
TraditionalForm[HoldForm[CenterDot[(1/n!) , 
AngleBracket[Style[Overscript[Underscript["", pt], n],  
ScriptSizeMultipliers -> 1]]]] == iid[pt, n]]]]]]

There is an undocumented function for the Eulerian: NumberTheory`EulerianNumber[n, k]. Note that the argument order in your version is reversed. — J. M.'s missing motivation, Nov 07 '15 at 07:27

Recursive piecewise integral relation with piecewise base case?

4 Answers4

Linked