PoincareSection for a driven damped pendulum is not generating a Poincaré section at all, why?

Question

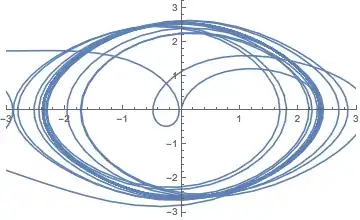
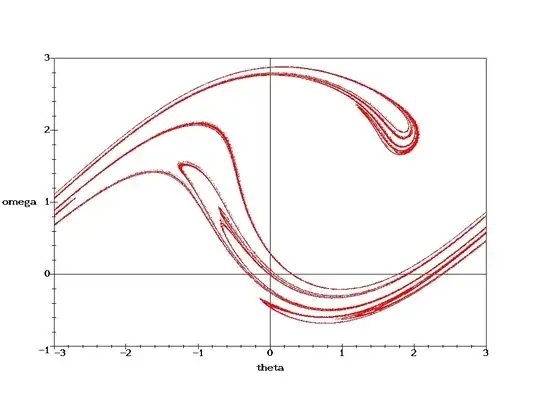
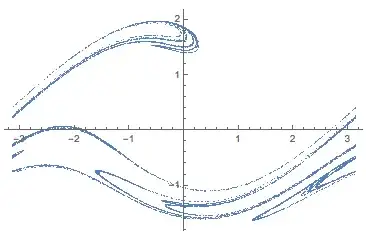
So I have the general code from the PoincareSection documentation that is changed up for a Driven Damped Pendulum:

coupledDiffEq = 
 {ω'[t] == -(1/q) ω[t] - Sin[θ[t]] + 
  g*Cos[ϕ[t]],
  θ'[t] == ω[t],
  ϕ'[t] ==  Drive};

data = Block[{q = 3.9, g = 1.5, Drive = 1}, 
Reap[NDSolve[{coupledDiffEq, 
θ[0] == 0, ω[0] == 0, ϕ[1] == 2*Pi, 
WhenEvent[Mod[ϕ[t], (2*Pi)] == 0, 
Sow[{θ[t], ω[t]}]]}, {}, {t, 0, 100000}, 
MaxSteps -> ∞]]][[-1, 1]];
ListLinePlot[data, PlotRange -> {{-3, 3}, All}]

Then I ListPlot data and it comes out as not a PoincareSection. Often it looks like a phase plot more than anything else. I have attempted to change the

Mod[ϕ[t], DriveFrequency]

where DriveFrequency should be Drive / (2*Pi), but that often does nothing. The system of equations evaluates and produces points, they just are random though. How do I get a nice Poincaré section with this?

I am getting this when I should be getting

Answer 1

Update

J.M. has some good comments, so I'm going to implement them.

coupledDiffEq = {θ''[t] == -(1/q) θ'[t] - 
 Sin[θ[t]] + g*Cos[ϕ[t]], ϕ'[t] == drive};

data = Block[{q = 3.9, g = 1.5, drive = 2/3}
   , First@Last@Reap@NDSolve[{
        coupledDiffEq, θ[0] == 0, θ'[0] == 0, ϕ[1] == 2 π
        , WhenEvent[Mod[ϕ[t], 2 π] == 0, Sow[{Mod[θ[t], 2 π, -π], θ'[t]}]]
        }, {}, {t, 0, 100000}, MaxSteps -> ∞]
   ];
ListPlot[Drop[data, 100]]

I dropped the first 100 points to make sure that we aren't capturing any of the transients.

---

I played around with your code, and couldn't get it to do what I wanted, so I went this route instead. Note that you need to move θ[t] back into the interval -π to π in order to get the attractor, and you should not use ListLinePlot, because you will get a mess.

ClearAll[coupledDiffEq, ω, q, θ, g, ϕ, drive]
coupledDiffEq := {ω'[t] == -(1/q) ω[t] - Sin[θ[t]] + g*Cos[ϕ[t]], θ'[t] == ω[t], ϕ'[t] == drive};

sols = Block[{q = 3.9, g = 1.5, drive = 2/3}
  , First@NDSolve[
     {coupledDiffEq, θ[0] == 0, ω[0] == 0, ϕ[1] == 2*π}
     , {θ[t], ω[t]}
     , {t, 0, 100000}
     , MaxSteps -> ∞
    ]
 ];

 data = Table[{Mod[θ[t] + π, 2 π] - π, ω[t]} /. sols, {t, 20*(2 π)/(2/3), 100000, (2 π)/(2/3)}];
 ListPlot[data, PlotRange -> All]

---

Update

This code should work too, more along the lines of what you did:

coupledDiffEq = {ω'[t] == -(1/q) ω[t] - Sin[θ[t]] + g*Cos[ϕ[t]], θ'[t] == ω[t], ϕ'[t] == drive};

sols = Block[{q = 3.9, g = 1.5, drive = 2/3}
  , First@Last@Reap@NDSolve[{coupledDiffEq, θ[0] == 0, ω[0] == 0, ϕ[1] == 2 π
  , WhenEvent[Mod[ϕ[t], 2 π] == 0, Sow[{Mod[θ[t] + π, 2 π] - π, ω[t]}]]
 }, {θ[t], ω[t]}, {t, 0, 100000}, MaxSteps -> ∞]];

ListPlot[sols]