Iterating a rational function

Question

I'm reading about iterating rational functions. I'm given $$R(z)=\frac{3z-2}{2z-1},$$ then the author makes the statement: "Then(by induction), $$R^n(z)=\frac{(2n+1)z-2n}{2nz-(2n-1)}.$$ Is there a simple way in Mathematica to produce $R^n(z)$?

Answer 1

As it turns out, RSolve[] is capable of handling this:

FullSimplify[RSolve[{f[n] == (3 f[n - 1] - 2)/(2 f[n - 1] - 1), f[0] == z},
                    f[n], n], n ∈ Integers]
   {{f[n] -> (2 n (-1 + z) + z)/(1 + 2 n (-1 + z))}}

---

Extra Credit

Explain the following observations:

f[n_, z_] := ((2 n + 1) z - 2 n)/(2 n z - (2 n - 1))

y /. First[Solve[z == f[n, y], y]] // Simplify
   (2 n + z - 2 n z)/(1 + 2 n - 2 n z)

f[-n, z] // Simplify
   (2 n + z - 2 n z)/(1 + 2 n - 2 n z)

Nest[f[1/2, #] &, z, 2] == f[1, z] // FullSimplify
   True

Answer 2

One way to solve this is to use FindSequenceFunction. First define the iteration

r[z_] := FullSimplify[(3 z - 2)/(2 z - 1)];

So that, for example, the first four terms are:

Nest[r, z, #] & /@ Range[4]

{(2 - 3 z)/(1 - 2 z), (4 - 5 z)/(3 - 4 z), (6 - 7 z)/(5 - 6 z), (8 - 9 z)/(7 - 8 z)}

To get the general form, feed several of these terms into FindSequenceFunction, which returns the answer as a pure function

sol = FindSequenceFunction[Nest[r, z, #] & /@ Range[10]]

(z - 2 #1 + 2 z #1)/(1 - 2 #1 + 2 z #1) &

Or in more familiar notation:

sol[n]

(-2 n + z + 2 n z)/(1 - 2 n + 2 n z)

Answer 3

This is not a proof, but I post it just for fun. In the following, the iterated Möbius transform is compared with the proposed solution in the complex plane and on the Riemann sphere...

spc[x_, y_] := {2 x, 2 y, -1 + x^2 + y^2}/(1 + x^2 + y^2)
mt[a_, b_, c_, d_][x_, y_] := 
 Through[{Re, Im}[(a x + a I y + b)/(c x + c I y + d)]].
fun = mt[3, -2, 2, -1]
g[n_] := mt[2 n + 1, -2 n, 2 n, -(2 n - 1)]
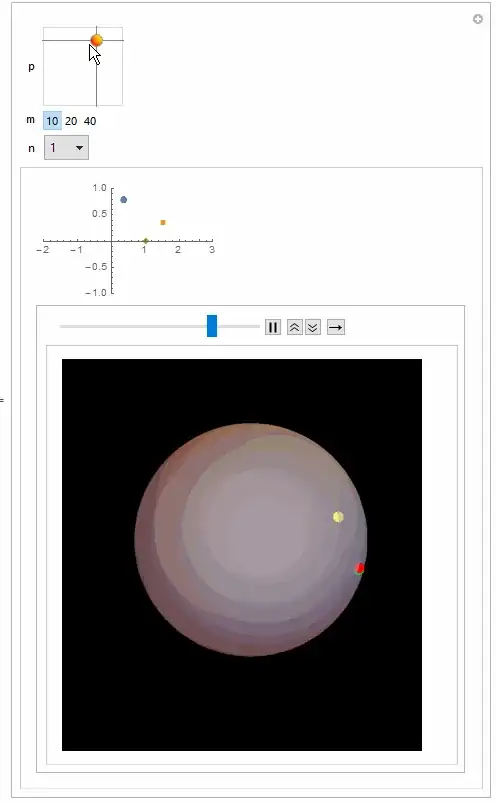
Manipulate[
 Column[{ListPlot[{{p}, {Nest[fun @@ # &, p, n]}, {g[m] @@ p}}, 
    PlotMarkers -> {Automatic, 10}, PlotRange -> {{-2, 3}, {-1, 1}}],
   ListAnimate[
    Graphics3D[{Opacity[0.5], Sphere[], PointSize[0.03], Opacity[1], 
        Yellow, Point[spc @@ p], Red, 
        Point[spc @@ (Nest[fun @@ # &, p, #])], , Green, 
        Point[spc @@ (g[m] @@ p)]}, Background -> Black, 
       Boxed -> False] & /@ Range[m]]}],
 {p, {-1, -1}, {1, 1}, Slider2D}, {m, {10, 20, 40}}, {{n, 1}, 
  Range[m], PopupMenu}]

The red point is the iterated function, and the green point the value of recursion solution at that iteration number.

Answer 4

I'm quite certain that the intention of the author (Alan Beardon?) is that you conjugate the function by the appropriate Möbius transformation to see that its dynamics are quite simple when looked at from the right angle. The process is pretty simple, but you can use Mathematica to assist, if desired.

The function has a single, repeated fixed point at $z=1$:

R[z_] = (3 z - 2)/(2 z - 1);
Solve[R[z] == z, z]

(* Out: {{z -> 1}, {z -> 1}} *)

The function should be simpler, if we conjugate it so that the fixed point is at $\infty$; that is, we conjugate by $\varphi(z)=1/(z-1)$:

phi[z_] = 1/(z - 1);
PHI[z_] = w /. First[Solve[phi[w] == z, w]];
Simplify[phi[R[PHI[z]]]]

(* Out: 2 + z *)

So, the dynamics of this function should be the same as just the simple shift $S(z) = z+2$. Of course, it's very simple to see that $S^n(z)=z+2n$. To find $R^n(z)$, we simply conjugate back:

S[z_] = z + 2 n;
r = Simplify[PHI[S[phi[z]]]]

(* Out: (2 n (-1 + z) + z)/(1 + 2 n (-1 + z)) *)