5

I'd like to generate triangular meshes or a cylinder and sphere primitives as part of a lattice meshing program I am writing to experiment with Mathematica. Consider the following snippet:

{p1, p2, r} = {{-1, 0, 0}, {1, 2, 1}, 0.5};
BoundaryDiscretizeGraphics[Cylinder[{p1, p2}, r]]
FullForm[%]
BoundaryDiscretizeGraphics[Sphere[p1, r], MaxCellMeasure -> 0.01]
FullForm[%]

I have 2 questions

  1. For the sphere: How can I extract the coordinates and connectivities I can see in the output of the second FullForm call into separate list of vertices and connectivities. I guess I need to do some magic to extract correct parts of the expression.

  2. For the cylinder: How can I convert the polygons defining the caps and the quadrilaterals around the body into triangles and then extract the triangles into vertices and connectivity lists as for the cylinder

enter image description here enter image description here

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
mkm
  • 223
  • 1
  • 6
  • 2
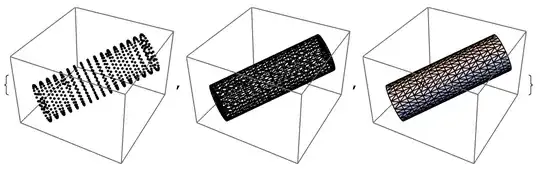
    How odd. It seems that even with a ridiculously small setting of MaxCellMeasure, the cylinder remains untriangulated... – J. M.'s missing motivation Nov 09 '15 at 23:09
  • 2
    @J.M. BoundaryDiscretizeGraphics doesn't triangulate flat surfaces (in contrast to DiscretizeGraphics). It is simply unnecessary for boundary approximation. – ybeltukov Nov 09 '15 at 23:28
  • 2
    Anyway: look up MeshCoordinates[] and MeshCells[]. – J. M.'s missing motivation Nov 10 '15 at 01:55
  • @J.M. Amazing, that's exactly what I want :) I knew it had to be something easy, but I didn't find those so I was thinking I would need some combination of Position[...,Heads->True] and Part[...], this is much easier though, thanks! – mkm Nov 10 '15 at 07:32

3 Answers3

4

Perhaps something like this:

Needs["NDSolve`FEM`"]
bmesh = ToBoundaryMesh[Cylinder[{p1, p2}, r], 
  RegionBounds[Cylinder[{p1, p2}, r]]]
bmesh["Wireframe"]

enter image description here

More information can be found on the ref page of ToBoundaryMesh.

user21
  • 39,710
  • 8
  • 110
  • 167
  • Nice, thanks for contributing, your solution is very concise! I slightly prefer my own though since for my lattice application I wanted to generate lots of bars each with a small number of elements. I should have mentioned that in the question. – mkm Nov 12 '15 at 07:47
  • 1
    @mkm, no worries if you want a more complicated solution I can come with one - not a very typical request though ;-) – user21 Nov 12 '15 at 07:55
  • haha, sure. The solution can have more elements, but the cylinder needs less, man! :) – mkm Nov 12 '15 at 08:08
2

For the first half of Question 2, use BoundaryDiscretizeRegion. For some reason it's important to avoid machine-precision Real numbers. Instead of 0.5, use arbitrary-precision Rational 1/2.

{p1, p2, r} = {{-1, 0, 0}, {1, 2, 1}, 1/2};
reg = BoundaryDiscretizeRegion[Cylinder[{p1, p2}, r]]

triangulated cylindrical surface

And yeah, as pointed out by J. M.♦ in the comment, MeshCoordinates and MeshCells are for the rest of your questions.

Array[Graphics3D[GraphicsComplex[MeshCoordinates[reg], MeshCells[reg, #]]] &, 3, 0]

extracting mesh elements

Community
  • 1
Taiki
  • 5,259
  • 26
  • 34
1

Using the tip from the comments I figured out the following solution

bdg = BoundaryDiscretizeGraphics[Cylinder[{p1, p2}, r]];

(* Triangulate boundary quads and cap polygons *)
cylinderPolyAll = Map[(#[[-1]]) &, MeshCells[bdg, 2], 1];
cylinderQuad = Select[cylinderPolyAll, (Length[#] == 4) &];
cylinderQuadE = 
  Flatten[Map[({#[[{1, 2, 3}]], #[[{3, 4, 1}]]}) &, cylinderQuad], 
   1];
cylinderCaps = Select[cylinderPolyAll, (Length[#] != 4) &];
cylinderCapsE = 
  Flatten[Map[(Table[{#[[1]], #[[i + 1]], #[[i + 2]]}, {i, 1, 
        Length[#] - 2}]) &, cylinderCaps], 1];

(* Vertices and connectivity of triangulated cylinder *)
cylinderE = Join[cylinderQuadE, cylinderCapsE];
cylinderV = MeshCoordinates[bdg];

(* Visualise triangulated cylinder *)
cylinderVE = With[{v = cylinderV, e = cylinderE}, Table[
    {v[[e[[i, 1]]]], v[[e[[i, 2]]]], v[[e[[i, 3]]]]},
    {i, 1, Length[cylinderE]}]];
Graphics3D[Map[Polygon[#] &, cylinderVE]];

enter image description here

The sphere case is easier

mkm
  • 223
  • 1
  • 6