Another approach that might be successful with some additional fine tuning.
pos = (pic = Import["https://i.stack.imgur.com/9uBnQ.png"]) //
Thinning // PixelValuePositions[#, 1] &;
center = Mean /@ Transpose[pos] // N;
out = Reap[
Module[{nextPos = {pos[[690]]}, newList = pos, delta = {-1., 1.},
lastPos = {pos[[690]]}},
Do[
{nextPos, newList} =
TakeDrop[newList,
First@Position[#,
First@MinimalBy[TakeSmallestBy[#, (Norm[#, 1] &), 5], (Norm[# + delta, 1] &)]] &
[Transpose[newList] - First@nextPos // Transpose]];
delta = (7*delta + 1*First[(lastPos - nextPos)] -
0.0039*First[({center} - lastPos)])/8.0039;
lastPos = Sow[nextPos];,
{866}
]
]][[2, 1]] ~Flatten~ 1;
One can use
Manipulate[
Show[{ListPlot[out[[;; n]], PlotMarkers -> {Automatic, 12}],
ListPlot[pos, PlotStyle -> Red]}, AspectRatio -> 1],
{n, 2, Length@out, 1}]
to explore the creation of out.
Trying to find an analytical function using FindFormula
formula =
FindFormula[#, PerformanceGoal -> "Quality",
SpecificityGoal -> "Low", TargetFunctions -> {Sin, Cos, Power, Plus, Times}] & /@
Transpose[out]
Plotting the results in comparison to the original data.
Show[{ListPlot[out, PlotStyle -> Gray, PlotMarkers -> {Automatic, 7}],
ListPlot[pos, PlotStyle -> Red, PlotMarkers -> {Automatic, 3}],
ParametricPlot[Through[formula[p]], {p, 1, Length@pos},
PlotStyle -> Hue[0.6]]},
AspectRatio -> 1]
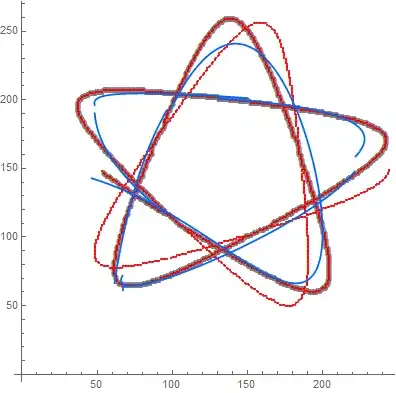
Show[pic, %]

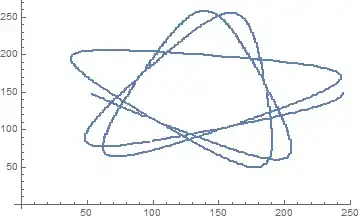
Show[ListPlot[Transpose@out],
Plot[Evaluate@Through[formula[x]], {x, 1, 1580}]]

ListPlot[{Reverse@out[[All, 1]], out[[All, 2]]}]






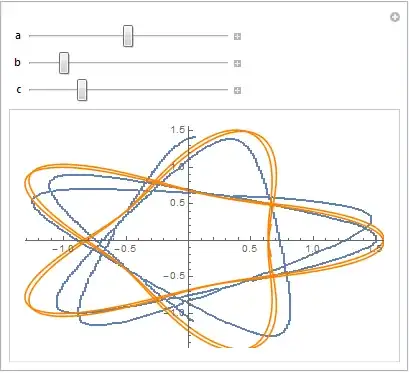
pospol = {ArcTan[#1, #2], Norm[{#1, #2}]} & @@@ N[pos]thenListPlot[pospol]. Note the periodic function which looks something likea Abs[Sin[b x + c]]^d + e, but also there is some drift in parameters – LLlAMnYP Nov 12 '15 at 11:37pos = (# - Mean@pos)&/@posto translate this to the origin. After all this and normalization I got the following plot: http://i.stack.imgur.com/TPQoH.png – LLlAMnYP Nov 12 '15 at 11:41