13

For glaucoma diagnosis it is common to determine a "cup to disk ratio" which compares the diameter of the optic disk (VDD) and optic cup (VCD). The optical disk is visible as a circular red feature (red channel) and the optic cup shows up as a yellow circle (green channel). How can I calculate the diameter ratio between optic disk and optic cup?

I am able to detect the optic disk with canny edge detection, but I have not found a way to calculate the cup to disk ratio. How might I do that?

enter image description here

dionys
  • 4,321
  • 1
  • 19
  • 46
indra ginanjar A.T
  • 173
  • 4
  • Can you provide sample images (without labeling) for experimentation? – kirma Nov 16 '15 at 12:53
  • 1
    Is your question more about how to automatically find the ellipse pattern in an image? or about fitting an ellipse at a starting point in an image? or more about calculating the size of the ellipse? Please provide a minimal example. – Thies Heidecke Nov 16 '15 at 12:55
  • You may also check this answer for ellipse fitting. http://mathematica.stackexchange.com/questions/25589/how-can-i-detect-an-ellipse-in-a-photo?rq=1 – s.s.o Nov 16 '15 at 13:04
  • how about calculating the diameter between optic disk and optic cup? sorry my first question is not complete. i have already detect the optic disk with canny edge detection, but i have not found a way to calculate the diameter of optic disk and optic cup. How might I do that? – indra ginanjar A.T Nov 16 '15 at 16:44
  • 1
    @kirma - Additional info and test images for glaucoma and related eye problems: optic-disc.org – dionys Nov 17 '15 at 12:40
  • Welcome to Mathematica.SE! I suggest the following: 0) Browse the common pitfalls question 1) As you receive help, try to give it too, by answering questions in your area of expertise. 2) Read the [faq]! 3) When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! – Dr. belisarius Nov 18 '15 at 15:30

2 Answers2

27

Fitting an ellipse:

i = Import["https://i.stack.imgur.com/W7HJk.jpg"];
lineByCenter[center_, semi_, angle_] := Rotate[Line[{#1 - #2, #1 + #2}], angle, #1]&
                                                                       [center,{0,semi}]
sa    = 1 /. ComponentMeasurements[ Binarize@i, "SemiAxes"]
angle = 1 /. ComponentMeasurements[ Binarize@i, "Orientation"]
bbc   = Mean /@  Last /@ ComponentMeasurements[ Binarize@i, "BoundingBox"] // First
Show[i, Graphics[{Thick, White, Rotate[Circle[bbc, sa], angle, bbc],
                          Blue, lineByCenter[bbc, sa[[1]], angle + Pi/2],
                         Green, lineByCenter[bbc, sa[[2]], angle]}]]

Mathematica graphics

edit

In your previous and now closed question you asked for a yellow "cup" and a red "disk".The problem is that the "cup" barely resembles a same-center ellipse, so you need to define some additional criteria.Look: 

i = Import["https://i.stack.imgur.com/W7HJk.jpg"];
s = ChanVeseBinarize[i, "TargetColor" -> {Yellow, Red}];
ImageMultiply[i, ColorNegate@s]

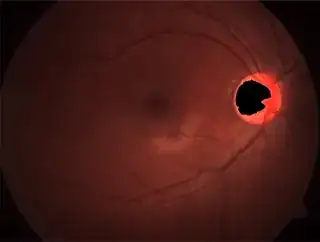
Mathematica graphics

edit2

After some googling I got convinced that the "cup" isn't really constrained to be a co-centered ellipse and the relevant parameters for the diagnosis/prognosis aren't just size measurements, but also the relative position of both components:

enter image description here

Dr. belisarius
  • 115,881
  • 13
  • 203
  • 453
18

If you need more precise calculation you may check this answer.

cm = ComponentMeasurements[Binarize@img, "BoundingDiskRadius"]
ct = 1 /. ComponentMeasurements[Binarize@img, "BoundingDiskCenter"];
Show[img, Graphics[{Thick, White, Circle[ct, cm[[1, 2]]]}]]

{1 -> 63.4933}

enter image description here

Community
  • 1
s.s.o
  • 4,559
  • 2
  • 27
  • 42