2D List Plot in a 3D box: What am I doing wrong?

Question

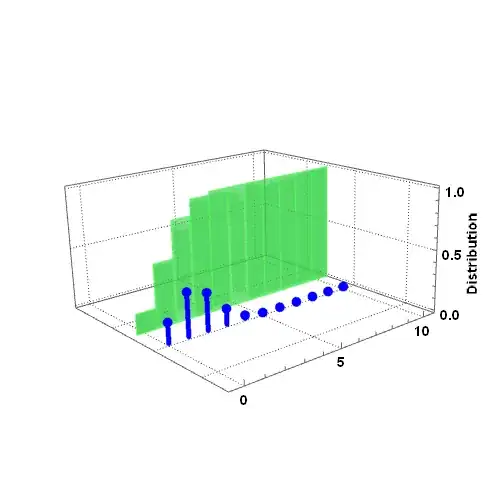
Let me just show the result first, and you'll see the error easily:

Now, this is just a 2D image sent into a 3D box, so you'd think they looked alike. But the 2D image behaves well:

The code was picked from an answer to a different question, here. I simplified it, and modified it to put in a list plot, so the final code looks like this:

p1 := Plot[{CDF[BinomialDistribution[5, 0.3], t], 0}, {t, 1, 4}, Filling -> {2 -> {{1}, {RGBColor[0.3, 1, 0.3, 0.6]}}}]
p2 := ListPlot[ Table[PDF[BinomialDistribution[5, 0.3], t], {t, 0, 10}], Filling -> Bottom, FillingStyle -> Directive[Thickness[0.01], Blue], PlotStyle -> Directive[PointSize[0.02], Blue]]

p2

Graphics3D[
 {
  p1[[1]] /. {x_?NumericQ, y_?NumericQ} :> {1, x, y},
  p2[[1]] /. {x_?NumericQ, y_?NumericQ} :> {2, x, y}
  }
 , Axes -> {True, False, True}, Boxed -> {Right, Bottom, Back}, BoxRatios -> {1, 1, 0.5}, FaceGrids -> {{0, 0, -1}, {0, 1, 0}, {1, 0, 0}}, FaceGridsStyle -> Directive[GrayLevel[0.3, 1], AbsoluteDashing[{1, 2}]], ViewPoint -> {-2, -2.5, 1}, AxesLabel -> {"Nothing, really", "", Rotate[Row[{Spacer[50], "Distribution"}], 90 Degree]}, LabelStyle -> Directive[Black, Bold, 14], ImageSize -> 500]

Can anyone see what causes the error? Is it my code, or does Mathematica have a funny bug here?

score 3 · Answer 1 · answered Nov 19 '15 at 22:31

I sometimes find it easier to reconstruct the plots from Graphics primitives, rather than messing with the internal structure of the Plot output.

Here is an idea:

discretes = Table[{t, 0, PDF[BinomialDistribution[5, 0.3], t]}, {t, 0, 10}];

Graphics3D[
 {
  (* PDF stems and points *)
  Blue, Thickness[0.01], PointSize[0.02], Point[discretes], 
  Line[{{#1, #2, #3}, {#1, #2, 0}}] & @@@ discretes,

  (* CDF *)
  Cases[
   DiscretePlot[
    CDF[BinomialDistribution[5, 0.3], t], {t, 0, 10},
    ExtentSize -> Full, FillingStyle -> RGBColor[0.3, 1, 0.3, 0.6], 
    PlotRange -> {0, Automatic}
   ],
   {directives__, Rectangle[{x0_, y0_}, {x1_, y1_}]} ->
    {Opacity[0.5, RGBColor[0.3, 1, 0.3, 0.6]], 
     EdgeForm[RGBColor[0.3, 1, 0.3, 0.6]], directives, 
     Cuboid[{x0, 1, y0}, {x1, 1, y1}]},
   Infinity
  ]
 },
 PlotRange -> {Automatic, {-3, 4}, Automatic},

 (* the directives below are from your original plot *)
 Axes -> {True, False, True}, Boxed -> {Right, Bottom, Back}, 
 BoxRatios -> {1, 1, 0.5},
 FaceGrids -> {{0, 0, -1}, {0, 1, 0}, {1, 0, 0}},
 FaceGridsStyle -> 
  Directive[GrayLevel[0.3, 1], AbsoluteDashing[{1, 2}]],
 ViewPoint -> {-2, -2.5, 1},
 AxesLabel -> {"", "", Rotate[Row[{Spacer[50], "Distribution"}], 90 Degree]}, 
 LabelStyle -> Directive[Black, Bold, 14], ImageSize -> 500
]

Mathematica graphics

score 1 · Answer 2 · answered Nov 19 '15 at 22:26

p2[[1]] contains a GraphicsComplex expression, and your replacement is affecting the integer coordinate indices as well as the coordinates themselves. So something like Line[{14, 3}] becomes Line[{2, 14, 3}] which is why you see the spurious extra line segments all sprouting from point number 2. A solution is simply to wrap p2[[1]] in Normal:

Graphics3D[{
  Normal[p2[[1]]] /. {x_?NumericQ, y_?NumericQ} :> {2, x, y}}, 
 BoxRatios -> {.1, 1, 1}]

That did the trick very quickly. Thank you! :-) – Svein Olav Nyberg Nov 20 '15 at 04:19 — Svein Olav Nyberg, Nov 20 '15 at 04:19

2D List Plot in a 3D box: What am I doing wrong?

2 Answers2