A delicate elementary inequality

Question

The following "piecewise-quadratic" inequality emerged in a joint work of Rom Pinchasi and myself. The inequality is surprisingly delicate, and all our attempts to simplify it made it false. By the end of the day, we were able to prove the inequality, but the proof is unreasonably sophisticated, totalling to about 15 pages. We would be happy to have a shorter proof.

The inequality involves the function $G$ of three real variables, defined as follows: if $(\xi,\eta,\zeta)$ is a non-decreasing rearrangement of $(x,y,z)$, then we let $$ G(x,y,z) := \begin{cases} \xi\eta &\ \text{if}\ \zeta\ge \xi+\eta, \\ \xi\eta-\frac14\,(\xi+\eta-\zeta)^2 &\ \text{if}\ \zeta\le \xi+\eta. \end{cases} $$ Thus, for instance, we have $G(9,6,7)=38$, whereas $G(7,14,6)=42$. Now consider the function $f$ of four variables defined by $$\begin{align*} f(x_0,x_1,y_0,y_1) &:= \min \{ 0.15s^2, x_0y_0+x_1y_1 \} \\ &\qquad + G(x_0,y_1,1-s) + G(x_1,y_0,1-s) \\ &\qquad + 0.25(1-s)^2, \end{align*}$$ where for brevity I write $s=x_0+x_1+y_0+y_1$, and let $$ \Omega := \{ (x_0,x_1,y_0,y_1)\in{\mathbb R}_{\ge 0}^4\colon 1/2 \le s \le 1. \}. $$ All we want to show is that $$ \max_\Omega f \le 0.15. $$ (Indeed, the maximum is actually equal to $0.15$: say, we have $f(0.5,0,0.5,0)=0.15$.)

---

At Pat Devlin's suggestion, here is the graph of the maximum as a function of the sum $s=x_0+x_1+y_0+y_1$.

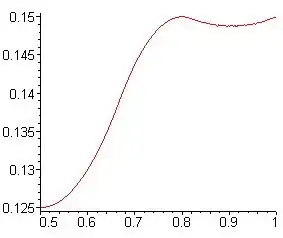
_{(source: haifa.ac.il)}

It looks nice, but does not seem to be a graph of some "simple" function; and so, there is probably no simple analytic expression for $\max f$ over all quadruples $(x_0,x_1,y_0,y_1)$ adding up to $s$.

Answer 1

The paper where the inequality in question emerged is, finally, written (and uploaded to the arXiv, in case anybody is interested). We were eventually able to simplify the proof and squeeze it down to just about six pages; indeed, the whole paper is now shorter than our original proof. I sketch very briefly the new proof below.

We start with the identity \begin{multline*} G((x+y)/2,(x+y)/2,z) = G(x,y,z) \\ + \frac14(x-y)^2 - \frac14 \big(\max\{|x-y|-z, 0 \} \big)^2. \tag{1} \end{multline*} Once stated, this is easy to verify by a careful case analysis. An immediate consequence is that $G(x,y,z)$ can only grow if both $x$ and $y$ are replaced with their average $(x+y)/2$.

As another preparation step, we exploit the internal symmetries of $f$ to assume, without loss of generality, that $$ x_0+x_1 \ge y_0+y_1 \tag{2} $$ and also $$ x_0+y_0 \ge x_1+y_1. \tag{3} $$

Our big plan is to investigate how $f$ changes under the balancing operation which includes replacing $x_0$ and $y_1$ with their average $(x_0+y_1)/2$ and, simultaneously, $x_1$ and $y_0$ with their average $(x_1+y_0)/2$. Using the identity (1), we could show that either $f$ is non-decreasing under such balancing, or, under the assumptions (2) and (3), we have \begin{align*} x_0 &\ge y_1+(1-s), \tag{4} \newline y_0 &\ge x_1+(1-s), \tag{5} \end{align*} and $$ 3(x_0+y_0)+(x_1+y_1) \ge 2. \tag{6} $$

The precise meaning of being non-decreasing under balancing is that $$ f(x_0,x_1,y_0,y_1) \le f(z_0,z_1,z_1,z_0), $$ where $z_0=(x_0+y_1)/2$ and $z_1=(x_1+y_0)/2$. Consequently, in this case the problem reduces to maximizing a function of just two variables, which is a feasible task.

Now, if $f$ is decreasing under balancing, then, in view of (4) and (5) and by the definition of the function $G$, we have $$ G(x_0,y_1,1-s) = y_1(1-s) \ \text{and}\ G(x_1,y_0,1-s)=x_1(1-s). $$ Hence, \begin{multline*} f(x_0,x_1,y_0,y_1) = \min\{0.15s^2,x_0y_0+x_1y_1\} \newline + (x_1+y_1)(1-s) + 0.25(1-s)^2. \end{multline*} The expression in the right-hand side is can only increase if $x_0$ and $y_0$ are both replaced with their average, and, simultaneously, $x_1$ and $y_1$ are replaced with their average. Consequently, we can assume that $x_0=y_0$ and $x_1=y_1$. This, again, reduces the problem to maximizing a function of two variables, which takes some two more pages to accomplish.