Measures of non-abelian-ness

Question

Let $G$ be a finite non-abelian group of $n$ elements. I would like a measure that intuitively captures the extent to which $G$ is non-commutative. One easy measure is a count of the non-commutative products. For example, for $S_3$, 9 products are non-commutative, or, 18 of the 36 entries in the multiplication table indicate non-commutivity (in the table, $r$=rotation; $f$=flip):
          
So one might say $S_3$ is 50% non-abelian.

Another idea is to determine the fewest element identifications needed to make the group abelian. If one identifies the elements $r$ and $r^2$ above, and calls the resulting merged element $a$, then I believe $S_3$ is reduced to the abelian $C_2$:
          
So one might say $S_3$ is one element identification away from being abelian.

My question is:

Is there some standard, accepted measure of how far a group is from being abelian?

Ideally such a measure would not be restricted to finite groups. Thanks for pointers!

Answer 1

Of course, one might say that both $Z(G)$ and $[G,G]$, in a sense, "measure" the non-commutativity of $G$. But they are not very good "quantitative" measures.

I think what you are aiming at is a notion introduced by Turán and Erdős (Some problems of a statistical group theory IV, Acta Math. Acad. of Sci. Hung. 19 (1968), 413-435), the "probability that two elements of $G$ commute": $$P(G) = \frac{\left|\{ (x,y)\in G\times G\mid xy=yx\}\right|}{|G|^2}.$$ In fact, $P(G) = k/|G|$, where $k$ is the number of conjugacy classes of $G$. Gustafson proved that if $G$ is nonabelian then $P(G)\leq 5/8$, and extended the notion to compact groups using Haar measure (W. Gustafson, What is the probability that two group elements commute? American Math. Monthly 80 (1973) 1031-1034). MacHale proved that certain values cannot occur: if $P(G)\gt \frac{1}{2}$, then $P(G) = \frac{1}{2} + \left(\frac{1}{2}\right)^{2s+1}$; and $P(G)$ cannot satisfy $\frac{7}{16} \lt P(G) \lt \frac{1}{2}$. Joseph proved that if $G$ is not commutative and $p$ is the smallest prime that divides $|G|$, then $P(G)\leq \frac{p^2+p-1}{p^3}$ (K.S. Joseph, Commutativity in non-abelian groups, PhD thesis, 1969, UCLA). There's been some other work on this.

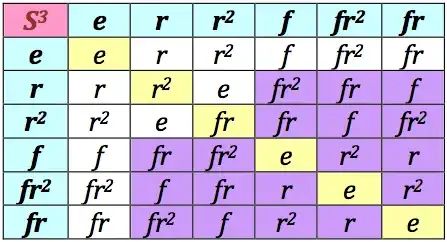
In the case of $S_3$. $|G|=6$, and the set of pairs $(x,y)$ with $xy=yx$ is, as you note, $18$, so the probability that two elements commutes is precisely your "50% nonabelian".

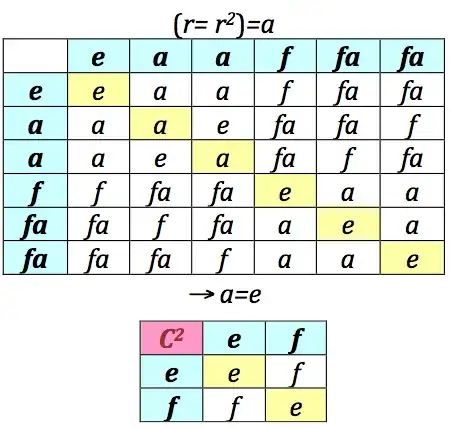
Your second notion seems to be that of looking at $G/[G,G]$, which is the "largest" quotient of $G$ which is abelian.

Added: Since I edited to fix the accent on Erdős, I'll take the opportunity to add some references:

• Desmond MacHale, How commutative can a non-commutative group be?, Math. Gazette 58 (1974), 299-202.
• David J. Rusin, What is the probability that two elements of a finite group commute?, Pacific J. Math 82 (1979), no. 1, 237-247.
• Robert Guralnick and Geoff Robinson, On the commuting probability in finite groups, J. Algebra 300 (2006), no. 2, 509-528, MR 2228209 (2007g:60011); Addendum, J. Algebra 319 (2008), no. 4, 1822.

Answer 2

You may want to look at the commutativity graph of a finite groups (vertices are elements, an edge connects $a$ and $b$ if $ab=ba$. This and similar graphs have been extensively studied. See, for example, this paper and the references there.

Answer 3

Yes, as Arturo says, you probably want what is known as the "commuting probability of $G$", cp(G). Bob Guralnick and I proved (among other things) in a Journal of Algebra paper (circa 2006) (without using the classification of finite simple groups) that $cp(G) \to 0$ as $[G:F(G)] \to \infty,$ where $F(G)$ is the largest nilpotent normal subgroup of a finite group $G,$ though sharper results are possible using the classification.

Answer 4

For certain applications, the abelian-ness of a group is inversely proportional to the quasirandom-ness of a group. The latter notion is more obscure, so this observation might not be a help at first. On the other hand quasirandom-ness can be measured quantitatively in a number of basically equivalent ways.

This is all laid out very beautifully in the paper Quasirandom groups by Tim Gowers. This is the first paper where the notion of a quasirandom group rears its head, and Gowers gives five equivalent definitions. Perhaps the most accessible is this: a group is $c$-quasirandom if the smallest dimension of a non-trivial irreducible representation is at least $c$. Obviously abelian groups are 1-quasirandom, but not 2-quasirandom; indeed, the same is true of all non-perfect groups.

On the other hand Gowers makes this remark about the family of groups $PSL_2(q)$:

...the order of $PSL_2(q)$ is $q(q^2 − 1)/2$, so the lowest dimension of a non-trivial representation is proportional to the cube root of the order of the group. This tells us that, in a certain sense, $PSL_2(q)$ is very far from being abelian.

Answer 5

I am not sure that the following will be useful, however...

Similarly to the answer of Mark Sapir let us consider the "anti-commutativity" graph (an edge connects $a$ and $b$ if $ab\ne ba$). Of course, it is not connected, and the number of its connected components can be taken as some measure of non-abelian-ness. E.g., this measure equals 2 (minimal value) for $S_n (n\ge 5)$.

Addendum: Morfeover, every simple group has the measure 2.

Answer 6

It seems that the same notions of "non-abelianness" also apply to semigroups. Should the notions somehow take into account the added structure a group has?