15

Can we have positive reals $x,y,z$ with $$ x^{\left( y^z \right)} = y^{\left( z^x \right)} = z^{\left( x^y \right)} $$ in cyclic permutation, other than the line $x=y=z$?

I put this at https://math.stackexchange.com/questions/493739/this-is-stupid-but-i-have-a-bad-cold-with-cough and one poor guy has been hacking away at it. I still have no idea.

I would love to see some representation of the supposed surface $$ x^{\left( y^z \right)} = y^{\left( z^x \right)}, $$ which I feel really ought to be some ugly variant of the helicoid around the line $x=y=z$.

EDIT, Thursday: Is it true that the gradient of $$ \color{magenta}{ h(x,y,z) = x^{\left( y^z \right)} - y^{\left( z^x \right)}}, $$ is defined and a nonzero vector along the line, say, at the point $x=y=z=t$ for positive real $t?$ If so, the surface is orthogonal to that at the line...Further, if you switch to one of the other pairs as a difference, I expect the gradient vector to be rotated by $120^\circ;$ this gives a pretty good reason for there being no other points on all three such surfaces near the known line.

Community
  • 1
Will Jagy
  • 25,349
  • Dear @Will Jagy: I removed the deprecated tag 'geometry' from this question. I do not know what to replace it with. Please feel free to add a more specific alternative tag. – Ricardo Andrade Oct 03 '13 at 04:05
  • 5
    I believe you have put your finger on the problem. My entire life is deprecated. – Will Jagy Oct 03 '13 at 04:38
  • 1
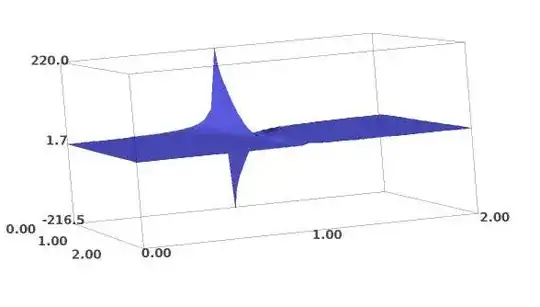
    Re: gradient. I suppose it is defined along the line and is indeed rotated when switching pairs. The gradient appears to be: -(t^(t + t^t + 1)*log(t)^2 - t^(t + t^t))/t , (t^(t + t^t + 1)*log(t) - t^(t + t^t))/t , t^(t + t^t)*log(t)^2 - t^(t + t^t)*log(t) – joro Oct 04 '13 at 06:03
  • A better parametrization is: y = exp(-LambertW(-z^(1-x)*ln(x))/z) – joro Oct 04 '13 at 10:46
  • @joro, is this last one a parametrization for a difference of two out of three, as in your "answer" – Will Jagy Oct 04 '13 at 18:19
  • Will, yes it is just for two of them. For the third we are looking for solutions to a single equation in x,y right after EDIT in my answer. – joro Oct 05 '13 at 05:09

2 Answers2

30

The following Maple-produced animation suggests that there isn't any other solution. The three curves (for each value of $x$) are $x^{y^z}=y^{z^x}$ (red), $y^{z^x}=z^{x^y}$ (blue) and $z^{x^y}=x^{y^z}$ (cyan). The one point in each frame where all three intersect is, of course, $x=y=z$. There don't appear to be any other triple intersections.

enter image description here

Robert Israel
  • 53,594
8

Maple found closed form for $z$ and parametrization over $\mathbb{C}$ for $x^{(y^z)}=y^{(z^x)}$:

$$ z= {{\rm e}^{ \left( -x{\it LambertW} \left( -\ln \left( y \right) { {\rm e}^{\ln \left( {\frac {\ln \left( x \right) }{\ln \left( y \right) }} \right) {x}^{-1}}}{x}^{-1} \right) +\ln \left( {\frac { \ln \left( x \right) }{\ln \left( y \right) }} \right) \right) {x}^ {-1}}} \qquad (1) $$

EDIT

Substituting $z$ in the other equation and solving, we are looking for positive real solutions of

x^exp(ln(y)*exp((-x*LambertW(-ln(y)/x*exp(ln(ln(x)/ln(y))/x))+ln(ln(x)/ln(y)))/x))-exp((-x*LambertW(-ln(y)/x*exp(ln(ln(x)/ln(y))/x))+ln(ln(x)/ln(y)))/x)^(x^y)

Complex solutions exist, e.g.

x1= (4.039760831390928810096443230122786460497 - 3.794516696260006267408154939005426227609j)
y1= (2.764005926356850384451036006794311106205 + 0.0j)
z1= (1.273990994985239416952018723391988170796 + 0.2830754921068781180566923204291057573632j)

Things get complicated by the fact that with the principal branches of $W$ and $\log$ $(1)$ need not be real and might have imaginary part.

Here is a plot of $(1)$ taking the principal branches and the real part. The plot is wrong because it has some artifacts caused by imaginary part.

Will try to make correct plot if I have the time.

Glorfindel
  • 2,743
joro
  • 24,174
  • I don't know anything about solutions over C. It would be informative to have the picture with $x,y > 1,$ where perhaps there is just one branch of everything. – Will Jagy Oct 03 '13 at 08:04
  • In particular, this plot contains the line $x=1, y=1$ with no bound on $z.$ So maybe $x > 1.1, y > 1.1$ – Will Jagy Oct 03 '13 at 08:18
  • @Will will make another picture. (2,5) has imaginary part, so branches still cause trouble... – joro Oct 03 '13 at 08:19
  • 1
    Huh. Oh, well. I certainly never expected to see any sort of formulaic solution for one of these. – Will Jagy Oct 03 '13 at 08:25
  • @WillJagy me too. Get numerical support over C for the paramatrization. – joro Oct 03 '13 at 08:29
  • @WillJagy edited the question with complex solutions and equation for the full problem. – joro Oct 03 '13 at 09:34
  • @WillJagy here is a plot from 1.1 to 9 (again wrong, maybe about half of it is correct): http://s9.postimg.org/472q3udr3/will2.jpg – joro Oct 03 '13 at 11:47
  • Another plot from 2 to 9 using root finding: http://s7.postimg.org/fdovi58kb/will4.png – joro Oct 03 '13 at 14:15
  • Joro, one thing would help me, for behavior near the line $x=y=z.$ Is it true that the gradient of $$ h(x,y,z) = x^{\left( y^z \right)} - y^{\left( z^x \right)}, $$ is defined and a nonzero vector along the line, say, at the point $x=y=z=t$ for positive real $t?$ If so, the surface is orthogonal to that at the line...Further, if you switch to one of the other pairs as a difference, I expect the gradient vector to be rotated by $120^\circ;$ this gives a pretty good reason for there being no other points on all three such surfaces near the known line. – Will Jagy Oct 03 '13 at 20:17