2

Let $\mathcal{P}$ be a finitely generated planar algebra.

Question : Is it also singly generated ?

I ask this question, because, on one hand I've read on this paper of V. Jones and D. Bisch :
"It thus makes sense to ask how many elements of $\mathcal{P}$ are required to generate $\mathcal{P}$ "

But on the other hand, if finitely many elements $(b_i)_{i \in I}$ generate $\mathcal{P}$, with $b_i \in V_{n_i}$ a $n_i$-box, then by using a "direct sum" planar tangle (with $N=\sum_{i \in I} n_i$) $$ T : \bigotimes_{i \in I} V_{n_i} \to V_{N}$$ we produce the $N$-box $B = T(\otimes_i b_i)$ : 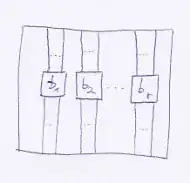enter image description here
which generate $\mathcal{P}$, because $\forall i$ we can generate $b_i$ (up to rescaling), by applying a "trace" planar tangle on all the $j \ne i$ components of the box $B$: 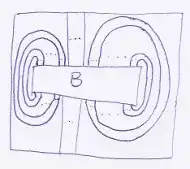enter image description here

I'm not an expert in planar algebra, perhaps this question is obvious, and perhaps this argument is trivially true or trivially false.

Sebastien Palcoux
  • 25,922

1 Answers1

4

Your answer will work, except if the $b_i$'s have trace zero as Theo points out. If the $b_i\in \mathcal{P}_{n_i}$ has trace zero, just use $1_{n_i}+b_i$ instead of $b_i$, where $1_{n_i}$ is $n_i$ parallel strands. Then you can cap this off to get a scalar as before. By what you remarked above, you'll be able to recover $1_{n_i}+b_i$, from which you can recover $b_i$ in the obvious way.

The above technique is used in Kodiyalam and Tupurani (arXiv:1003.4577), where they show all finite depth subfactors are singly generated. A more interesting question would be to find the smallest depth at which such a planar algebra is singly generated.

Dave Penneys
  • 5,335
  • Thank you Dave! About your question, the $2221$ subfactor planar algebra (of depth $4$) is known to be generated by two $3$-box, so it's generated be a single $6$-box. Is it known whether or not, it's also generated by a single $r$-box with $r<6$, and what's the smallest $r$ ? – Sebastien Palcoux Nov 21 '13 at 21:46
  • 1
    In fact, 2221 is singly generated by a 3-box. Just look at the planar algebra generated by one of the 3-boxes. There's no multiplicity 2 subfactor at that index (we would have seen it in the classification), so it must be 2221. – Dave Penneys Nov 21 '13 at 22:28
  • You're right! In R. Han thesis, page 48, theorem 5.0.16 (R3(T)) : $T^2 = f^{(3)} + \frac{Z(T^3)}{[4]}T + \frac{Z(QT^2)}{[4]}Q $, so we obtain $Q$ from $T$. – Sebastien Palcoux Nov 21 '13 at 22:42
  • I would like to formulate a conjecture like "a depth $n$ subfactor is cyclic iff its planar algebra is generated by a single $n$-box", but I don't know yet if it's relevant. – Sebastien Palcoux Nov 21 '13 at 22:52
  • 1
    I think that's not true. Look at the $\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$ subfactor. If I call the minimal projections at depth 2 $P$,$Q$,$R$, then $P-Q$ generates the planar algebra, since if I square it, I get $P+Q$, so I can recover $P$ and $Q$, and using $f^{(2)}$, I can recover $R$. But this group is not cyclic. – Dave Penneys Nov 21 '13 at 23:07
  • If I understand well, the space $\mathcal{P}_2$ is here $4$-dim. and its Temperley-Lieb part is $2$-dim., so its orthogonal is also $2$-dim. : $\mathbb{C}P \oplus \mathbb{C}Q$ (?), generated by the single $2$-box P−Q, as you write. – Sebastien Palcoux Nov 22 '13 at 11:01
  • I seems that every group subfactor planar algebra is generated by a single $2$-box, because if $P_1,...,P_m$ are orthogonal projections and $\zeta_m = e^{2i\pi /m}$ then I suspect $\sum \zeta^{k}_{m} P_k$ to generate every $P_k$ (as for $P-Q$ generate $P$ and $Q$). If it's true, I don't know yet how translate the property of being 'cyclic' for a subfactor, into a property of the planar algebra, but I hope it's possible. – Sebastien Palcoux Nov 22 '13 at 11:03
  • Andre wrote a proof here that the finite dimensional von Neumamn algebras are singly generated. Is this really prove that the depth $k$ subfactor planar algebras are generated by a single $k$-box ? And what about the example 8 page 4 of this paper ? – Sebastien Palcoux Nov 23 '13 at 22:22