Magic squares (Wiki) and Multiplicative magic squares (Wiki) are famous.
In this question, let us suppose that we do not consider the diagonals of multiplicative magic squares. Let us call such mulitplicative magic squares "multiplicative semi-magic squares".
The following square, for example, is one of $3\times 3$ multiplicative semi-magic squares.
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $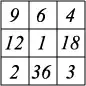
Note that $9\times 1\times 3\not=9\times 6\times 4$.
Here, suppose that all of the $N^2$ elements of each $N\times N$ multiplicative semi-magic square are distinct natural numbers. Also, let $M$ be the max of $N^2$ elements of the multiplicative semi-magic squares. Then, here is my question.
Question : What is the min $M_N$ of $M$ for $N\ge 6$? Can we represent them by $N$? Or can we find a good estimate of them?
I would like to know any relevant references.
Motivation : I've been interested in this question. I've already got the following :
$$M_3=15, M_4=27, M_5=45.$$
The followings are some of such squares.
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $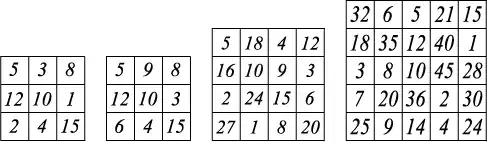
I've been able to prove that the above two sets of $3\times 3$ are the only sets such that $M=15$.
Remark : Please note that this question is not about the smallest possible magic products $P$ which has been studied (it is known that the smallest possible semi-magic product of $3\times 3$ is $120$). You can find a lot of information about this in the following page.