31

Problem: is it possible to dissect the interior of a circle into a finite number of congruent pieces (mirror images are fine) such that some neighbourhood of the origin is contained in just one of the pieces?

It may be conceivable that there is some dissection into immeasurable sets that does this. So a possible additional constraint would be that the pieces are connected, or at least the union of connected spaces.

A weaker statement, also unresolved : is it possible to dissect a circle into congruent pieces such that a union of some of the pieces is a connected neighbourhood of the origin that contains no points of the boundary of the circle?

This is doing the rounds amongst the grads in my department. So far no one has had anything particularly enlightening to say - a proof/counterexample of any of these statements, or any other partial result in the right direction would be much obliged!

Edit: Kevin Buzzard points out in the comments that this is listed as an open problem in Croft, Falconer, and Guy's Unsolved Problems in Geometry (see the bottom of page 87).

Anton Geraschenko
  • 23,718
sobe86
  • 375
  • 10
    The first question is listed as an unsolved problem in "Unsolved problems in geometry" by Croft, Falconer and Guy (section C6). So unless anyone has any recent news, you're probably not going to see a solution posted here. PS I am not an "unsolved problems in geometry" guru---I just googled for 'cutting a circle into congruent pieces' (without quotes) to see if there were any interesting examples on the web and it led me straight to the book. – Kevin Buzzard Mar 06 '10 at 20:44
  • Fair enough I guess. THe second problem follows from some thoughts of my own about the problem, and I think there might well be a way to do it, so any thoughts are welcome! – sobe86 Mar 06 '10 at 20:49
  • 1
    I should probably also share this link: http://forums.xkcd.com/viewtopic.php?f=3&t=27963 the users there decided the first problem was 'probably impossible', but no major progress was made on a proof...

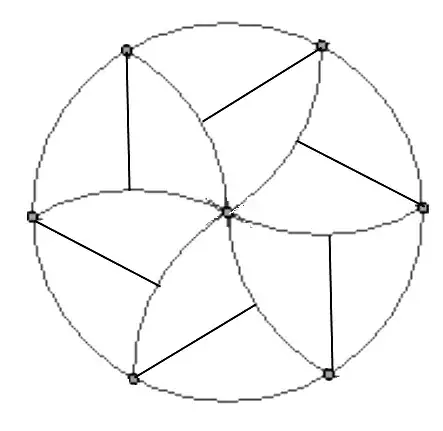
    This diagram is an example of a near miss for the second problem: http://i.imgur.com/iOfRI.png . This is why I think it may be possible...

     – sobe86 Mar 06 '10 at 20:51
  • The diagram is also in Croft-Falconer-Guy. If you really want to know about this problem you could do worse than getting hold of the book and finding out what else is said about it... – Kevin Buzzard Mar 06 '10 at 22:24
  • 1
    Please edit the title to reflect the question. "Is it possible to dissect the circle into congruent pieces, so that a neighborhood of the origin is contained within a single piece?" is plenty short enough to fit in a title. – Theo Johnson-Freyd Mar 07 '10 at 01:02
  • 1
    Actually, "disk" would be a much better word that "circle". – Theo Johnson-Freyd Mar 07 '10 at 01:03
  • 1
    I think the question should be edited to incorporate Kevins comments about the first question being listed as an open problem in Croft, Falconer and Guy. – GMRA Mar 07 '10 at 01:16
  • I edited a la Theo's post and put in the tag 'open problem'. – sobe86 Mar 07 '10 at 02:36

2 Answers2

21

A new paper was posted to the arXiv on related questions: "Infinite families of monohedral disk tilings," by Joel Haddley and Stephen Worsley (arXiv abs.). Here are tilings of the disk into congruent pieces where at least one piece does not touch the center (a result mentioned by Anton Geraschenko):

Fig.2
They conjecture (with extensive support) that,

"for any monohedral tiling of the disk, the centre may only intersect a tile at a vertex."

This would answer the original posed question in the negative.

Community
  • 1
Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • 5
    So the second tiling ($D_3^1$) answers the weaker question in the affirmative, right? – Fan Zheng Apr 29 '16 at 23:02
  • 1
    @FanZheng: The weaker question: "Is it possible to dissect a circle into congruent pieces such that a union of some of the pieces is a connected neighbourhood of the origin that contains no points of the boundary of the circle?" Excellent observation, Fan: Indeed you are correct. – Joseph O'Rourke Apr 29 '16 at 23:07
15

Given that this is an open problem, I figured I may as well make these comments an "answer".

Here's a related problem that I don't know how to answer:

1. Is any dissection of the disk into a finite number of congruent pieces rotationally symmetric?

It seems likely (to me) that any example of a dissection into a finite number of congruent pieces so that the center is in the interior of one of them is going to fail to be rotationally symmetric.

Actually, there's an easier problem that I don't know the answer to:

2. Is every dissection of the disk into a finite number of congruent pieces one of the following?

  • Slices of pizza. (i.e. every two pieces are congruent via a rotation around the center of the circle)
  • This one:
Anton Geraschenko
  • 23,718