21

Question. For which $N$ it is possible to cut a regular $N$-gon into congruent pieces such that the center of the regular polygon lies strictly inside one of the pieces? For $N=3,4$ there are trivial examples. For $N=6$ there is a nontrivial example by Peter Mueller (based on idea of Matt F.) below.

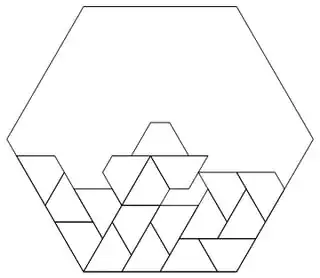
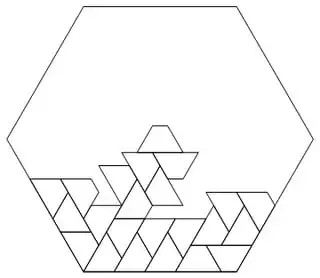
enter image description here

Remark. There is also similar open problem about a disc. Is it possible to dissect a disk into congruent pieces, so that a neighborhood of the origin is contained within a single piece? It seems that the answer is NO, but there is no proof.

Fedor Nilov
  • 663
  • 3
  • 9
  • $N=1, 6$ are OK? Do you know any $N$ for which it is not possible? – markvs Jul 13 '21 at 08:52
  • No, I don't know any $N$ for which it is impossible. What is a regular $1$-gon? Do you have an example of such cutting for $N=6$? – Fedor Nilov Jul 13 '21 at 09:01
  • Regular 1-gon (or 2-gon) is an interval. Honey-comb lattice cuts a hexagon.I did not think about $N=5$. – markvs Jul 13 '21 at 11:17
  • How is it possible to tile a hexagon using honeycomb? – Fedor Nilov Jul 13 '21 at 11:22
  • No it is not possible. Sorry! – markvs Jul 13 '21 at 11:36
  • It seems that for $N \neq 3,4$ such tiling is impossible. – Fedor Nilov Jul 13 '21 at 11:38
  • Perhaps you should emphasize that the center should be "strictly inside" one of the pieces. – Joseph O'Rourke Jul 13 '21 at 11:39
  • @JosephO'Rourke Done. Thank you! – Fedor Nilov Jul 13 '21 at 11:44
  • 3
    Can we cut a hexagon into diamonds (where a diamond is two equilateral triangles glued together on a side), with the center of the hexagon in the middle of some diamond, and an even number of diamond side-lengths on each side of the hexagon? Constructions like this give me hope: https://mathoverflow.net/a/349197/44143 –  Jul 13 '21 at 11:54
  • 2
    @MattF. If we cut each diamond into two pieces, then we have cutting of the hexagon into equilateral triangles with the same vertices as diamonds. And the center of the hexagon coincides with a vertex of some triangle. – Fedor Nilov Jul 13 '21 at 12:31
  • I take it "equal pieces" means congruent (not just, say, equal area). – Gerry Myerson Jul 13 '21 at 14:07
  • 1
    Done, thank you – Fedor Nilov Jul 13 '21 at 14:24
  • @MattF. Pieces may have different shapes, not necessary polygons. Could you give a figure of cutting, if you have an example? – Fedor Nilov Jul 14 '21 at 14:13
  • Could the underlying reason behind the imposibility of obtaining a tiling as proposed be the fact that the inner angles of every regular $N$-gon for $N>4$ are not divisors of 180°? It seems so to me, although I am far from having a proof. Which are your arguments for guessing that the answer is negative? – Juan Moreno Jul 17 '21 at 22:00
  • @JuanMoreno No arguments, just intuition. – Fedor Nilov Jul 21 '21 at 16:03
  • I wonder if this problem can be approached from the following view: Find a shape that can tile the plane, tile the half plane and tile a "half pane" with a $\frac{(N-2)180}{N}$ angle at 0. Then solve all the tiling problems at the edges and vertices of the N-gon locally with possible very small pieces. Finally connect the tilings using the plane tiling capability. If the pieces are small enough perhaps one can always "make it fit". – Robert Wegner Nov 04 '21 at 09:17
  • The necessary key result would be that any partial tilings can be connected if they are sufficiently far away from eachother and sit on a certain grid. – Robert Wegner Nov 04 '21 at 09:35

3 Answers3

22

Using the tiles suggested in Matt F.'s answer, there is a solution for the regular $6$-gon: enter image description here

Peter Mueller
  • 20,764
  • 1
    I guess you had a faster algorithm than I did! –  Nov 03 '21 at 14:34
  • 1
    @PeterMueller great! For you the bounty, and thanks for unblocking the problem! I observe that each tile is formed by eight equilateral triangles, so at the end the hexagon is cut in equilateral triangles with the center of the hexagon at the vertex of some of those triangles. Good strategy! – Juan Moreno Nov 03 '21 at 14:57
  • 3
    @MattF. I used a straightforward binary linear program formulation of the problem, which 'gurobi' can solve in a few seconds. But also the open source solver 'scip' takes less than 3 minutes. – Peter Mueller Nov 03 '21 at 15:22
  • @PeterMueller Beautiful example! – Fedor Nilov Nov 03 '21 at 19:31
  • 1
    Very nice! Did your computation verify that there is no such tiling with fewer than 108 trapezoids? – Timothy Chow Nov 03 '21 at 23:04
  • @TimothyChow For trapezoids of this shape (side lengths 1-2-3-2) I confirmed what Matt F. already did in his answer, that there is no such covering. (Note that the number of trapezoids in a cover of a hexagon of side length $n$ is $3n^2/4$, so $n$ is even.) – Peter Mueller Nov 04 '21 at 08:05
  • You should try tp get solutions for N = m6 via the following method: Rotate the whole hexagon by a number of degrees and overlay it on to the original. Do this m times so the outline becomes a star shape with 6m pointy vertices. "Cut" at all lines to have a completely new subdivision. Try to find a regular subdivision of the initial piece which admits all the new shapes to be made and hopefully doesnr cause the central piece to now have an edge intersecting 0. Use the new smaller pieces to fill in the remains to go from the star to the 6*m-gon. – Robert Wegner Nov 04 '21 at 09:03
  • 1
    What a beautiful picture! Only I wish it didn't have the red lines. – Yaakov Baruch Nov 05 '21 at 10:22
  • 1
    @YaakovBaruch OK, here is a version without the red lines :-) – Peter Mueller Nov 05 '21 at 14:57
6

Here are some partial results towards a negative answer.

For $N=6$, I tried solving this using a small trapezoidal tile, with side lengths of $2, 1, 2, 3$. For instance, here are some partial coverings with this tile on hexagons of side lengths $4, 6, 8, 10$. enter image description here enter image description here enter image description here enter image description here

For each of these hexagons, I conclude by exhaustive search that no covering by these tiles can put the center of the hexagon properly inside a tile.

One negative result in this area is Monsky's theorem, that there is no dissection of a square into an odd number of triangles of equal area. Perhaps some variant would give a negative answer to this question too.

0

Partial answer

I put here my thoughts about this problem. Please excuse the lack of formalization if any.

The possibility to cut a regular $N$-gon such that $N>4$ into congruent pieces such that the center of the regular polygon lies strictly inside one of the pieces is limited by the following facts:

  • (1) For $N>4$, the central angles $\alpha(N)$ of any regular $N$-gon are smaller than its inner angles $\beta(N)$. This can be easily checked, as $\alpha(N)=\frac{360}{N}$ and $\beta(N)=\frac{(N-2)*180}{N}$, so $\frac{\alpha(N)}{\beta(N)}=\frac{2}{N-2}$, which is lesser than $1$ for $N>4$

  • (2) Some regular $N$-gon is divisible in pieces $P$ only if one of the inner angles of $P$ divides exactly $\beta(N)$. Otherwise, there would be created an "empty" space that can not be filled with pieces $P$

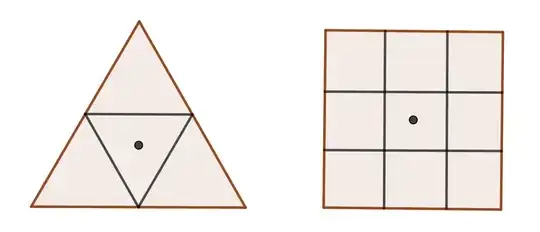
This facts prevent some regular $N$-gon such that $N>4$ to be cut in pieces $P$ such that $P$ is some regular polygon. For any regular polygon $P$ of $N>4$, fact (1) would imply the creation of some "empty" space by the polygons $P$ adjacent to the polygon $P$ with the center of $N$ strictly inside, that can not be filled with polygons $P$. Fact (2) let us discard also cutting any regular $N$-gon with squares, as no $\beta(N)$ is divisible by 90º; and finally, it can also be discarded cutting any regular $N$-gon with equilateral triangles for the same reason, with the exception of the hexagon; but in this case, the symmetries of the bisection of the inner angles disallows that the center of the hexagon lies strictly inside one of the triangles.

It would remain to show that using some non-regular piece $P$ is not possible for any regular $N$-gon. Fact (2) forces some inner angle of any piece $P$ to be greater than 90º (and thus such that it does not divide $\beta(n)$), which I believe that eventually leads to the creation of "empty" spaces that can not be filled with pieces $P$, but I am still working on a more formal proof.

Juan Moreno
  • 229