For which $n$ is it possible to find a permutation of the numbers from $1$ to $n$ such that the sum of any two adjacent elements of the permutation is a prime?
For example: For $n=4$ the permutation $(1,2,3,4)$ has sums $1+2=3$, $2+3=5$, $3+4=7$,and $4+1=5$.
For $n=16$ the permutation $(1,2,3,4,7,6,5,14,15,16,13,10,9,8,11,12)$ has sums of adjacent elements $(3,5,7,11,13,11,19,29,31,29,23,19,17,19,23,13)$.
Here are constructions with few sums.
The permutation $(12, 1, 10, 3, 8, 5, 6, 7, 4, 9, 2, 11)$ has adjacent sums equal to $11$, $13$, or $23$.
The permutation $(12, 1, 10, 3, 8, 5, 6, 7, 4, 9, 2, 11, 18, 13, 16, 15, 14, 17)$ has adjacent sums equal to $11$, $13$,$29$, or $31$.
If you have two pairs of twin primes $p$, $p+2$, $q$, $q+2$ with $q \gt 2p$ then the permutation of $q-p$
$$(p+1, 1, p-1, 3, ... p-2, 2, p, \\ q-p, p+2, q-p-2, p+4, ... p+5, q-p-3, p+3, q-p-1 )$$ has sums in $\{p,p+2,q,q+2\}$.
Heuristically, all but finitely many even numbers $n$ [Edit: that are divisible by $6$, as Aaron Meyerowitz and Mario Carneiro pointed out] should be expressible as a difference between a twin prime $p$ and a twin prime $q$ so that $q \gt 2p$.
Suppose we make a graph $G$ as in Moritz's answer. The number of edges is then $a_n=\sum_{p < n \text{ prime }}(p-1)/2$, which is asymptotic to $n^2/(2\log(n))$ by the prime number theorem. Now put $b_n=\lfloor n\log(n)\rfloor$, which is much smaller than $a_n$ when $n$ is large. It is a theorem of Pósa (see http://www.cs.utoronto.ca/~gbrunet/project2.pdf, for example) that a random graph with $b_n$ edges almost surely has a Hamiltonian cycle. (More precisely, if we let $g_n$ denote the number of graphs on $\{1,\dotsc,n\}$ with $b_n$ edges, and let $h_n$ denote the number that have a Hamiltonian cycle, then $h_n/g_n\to 1$ as $n\to\infty$.) This remains true even if we replace $b_n$ by $\lfloor cn\log(n)\rfloor$ for some $c>0$. As $a_n\gg b_n$ for large $n$, and there do not seem to be any very small counterexamples, it seems quite likely that there is a Hamiltonian cycle for all even $n$.
I am not quite sure what notation of cycles you use, but to investigate this question for small $n$ you could do the following. Build a graph $G$ with vertices $1,\dots,n$ and edges $\{i,j\}$ whenever $i+j$ is prime. Then you seem to be looking for Hamiltonian cycles in that graph. Here is what you get for some small n:
n
4 [1, 2, 3, 4]
6 [1, 4, 3, 2, 5, 6]
8 [1, 2, 5, 8, 3, 4, 7, 6]
10 [1, 4, 7, 10, 3, 2, 9, 8, 5, 6]
12 [1, 10, 3, 8, 11, 12, 7, 6, 5, 2, 9, 4]
14 [1, 10, 3, 2, 5, 14, 9, 8, 11, 12, 7, 4, 13, 6]
16 [1, 12, 7, 16, 15, 14, 9, 8, 5, 2, 11, 6, 13, 10, 3, 4]
18 [1, 18, 11, 8, 15, 16, 13, 6, 7, 12, 17, 2, 5, 14, 9, 10, 3, 4]
20 [1, 2, 9, 10, 3, 20, 11, 8, 5, 18, 19, 12, 17, 14, 15, 16, 7, 6, 13, 4]
22 [1, 2, 9, 22, 7, 4, 15, 8, 3, 10, 13, 16, 21, 20, 17, 14, 5, 6, 11, 18, 19, 12]
24 [1, 10, 3, 20, 23, 14, 9, 4, 7, 12, 19, 24, 13, 16, 21, 22, 15, 8, 5, 2, 17, 6, 11, 18]
26 [1, 16, 25, 12, 5, 14, 15, 22, 9, 8, 3, 26, 21, 20, 23, 24, 17, 2, 11, 6, 13, 18, 19, 4, 7, 10]
28 [1, 18, 23, 24, 19, 4, 27, 2, 17, 14, 15, 26, 11, 8, 5, 12, 7, 16, 21, 22, 25, 28, 9, 20, 3, 10, 13, 6]
30 [1, 16, 13, 18, 23, 20, 3, 10, 27, 26, 15, 8, 29, 30, 11, 2, 21, 22, 9, 28, 25, 12, 5, 14, 17, 24, 19, 4, 7, 6]
32 [1, 16, 21, 2, 17, 14, 29, 30, 31, 6, 7, 22, 25, 28, 15, 26, 3, 10, 13, 4, 27, 32, 5, 8, 9, 20, 23, 24, 19, 12, 11, 18]
So for small even $n$ there always seem to be such strings, and for no small odd $n$. See my comment for an explanation why odd is never possible.
It might seem plausible that the answer to your question could be: for the even n. (At least this is true for all $n$ up to 1000. This can be checked by finding the Hamiltonian cycles with backtracking). For a random graph with $O(n\log n)$ edges, the probability to contain a Hamiltonian cycle tends to $1$. If the edges you prescribe behave randomly for even $n$ and there are more of them, then the result seems plausible.
Of course this method can be adapted to simliar situation, when your are looking for the difference being prime or the sums belonging to some other set (e.g. fewer primes).
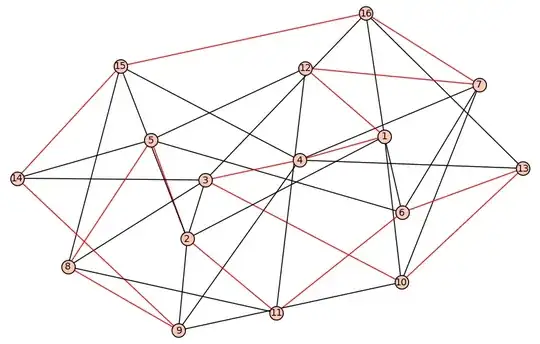
I attach a picture for the graph and the Hamiltonian cycle for $n=16$.
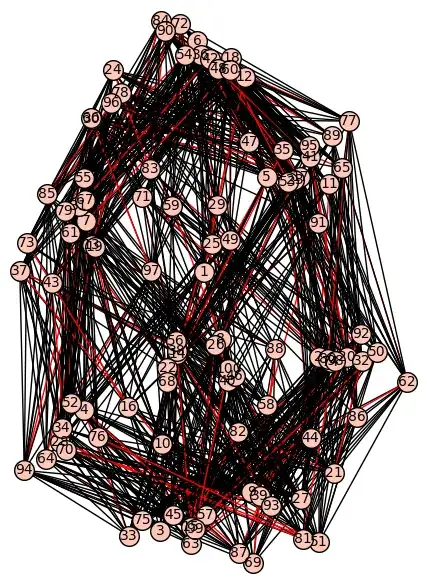
For larger $n$ such picture are less useful. For example for here is a picture for $n=100$.
Here is a construction that allowed me to verify with a few minutes of computer time that such cycles exist for all even $N \leq 10^{12}$. Let $G_n$ be the "prime-sum" graph with vertices labeled $1,\dots,n$ and edges connecting numbers that sum to a prime. First notice that if $N$ is even and there is a twin prime pair $N+2k-1$ and $N+2k+1$ with $2k<N$, then there is a path in $G_N$ from $2k-1$ to $2k$ that includes all larger numbers up to $N$ (just follow the edges that correspond to sums $N+2k-1$ and $N+2k+1$). So if there is a hamilton path in $G_{2k}$ from $2k-1$ to $2k$, then combining these two paths yields a hamilton cycle in $G_N$.
It is relatively straightforward to construct inductively such hamilton paths for $2k<10^7$, again using twin primes. If $2k-1$ and $2k+1$ are prime, the edges of those two sums immediately yield the desired path (this would give Douglas Zare's construction). Otherwise let $2k+a-1, 2k+a+1$ be the next twin prime pair. The edges corresponding to these two sums will give a path from $2k-1$ to $2k$ leaving out only the numbers $1,\dots, a$. Assuming that we already obtained a hamilton path from $a-1$ to $a$ in $G_a$, we can now "glue" that path to the path from $2k-1$ to $2k$ by replacing an appropriate edge. Alternatively we can use the hamilton path from $a+1$ to $a+2$ in $G_{a+2}$ and "glue" with two suitably chosen edges.
This means that whenever $N$ is even and there is a twin prime pair larger than $N$ and within distance $10^7$, there is a hamilton cycle in $G_N$. We can therefore check the existence of such hamilton cycles for $N\leq 10^{12}$ (and probably way larger) by finding a sequence of twin prime pairs with distances just below $10^7$, without performing any calculations for individual values of $N$.
EDIT: A modification of this argument shows that there are infinitely many values of $N$ for which $G_N$ is hamiltonian.
If $N+1$ and $N+2k+1$ are prime, we can use all edges with these two sums to obtain a collection of $k$ paths that start and end in $\{1,\dots, 2k\}$ so that for each path, the sum of the two endpoints is congruent to $N+1$ modulo $2k$.
By the famous theorem of Zhang, Maynard, Tao and others (Polymath 8a, 8b) on bounded gaps between primes, there are infinitely many $N$ for which this holds with $2k\leq 246$.
We can now check that for each $k\leq 123$ and each possible congruence class of $N$ modulo $2k$ (the even classes), these paths can be combined with $k$ more edges (matching $1, 3, 5,\dots, 2k-1$ to $2,4,6,\dots, 2k$) into a hamilton cycle. With only one exception, this completion can be obtained by taking either the edges that sum to $2k+1$ or the edges that sum to two primes of the form $p$ and $p+2k$.
The only exception is when $2k=20$ and $N\equiv 6$ (mod 20). In that case the long paths will connect numbers in $\{1,\dots,20\}$ that sum to 7 or 27, and none of the three prime-pairs $(3, 23)$, $(11, 31)$ or $(17, 37)$ will connect them into a single cycle. But it is easy to find an ad-hoc solution to that single case.
The question is not new. In fact, in 1982 Antonio Filz [J. Recreational Math. 14(1982), p.64] conjectured that for any $n = 2,4,6,\ldots$ there is a circular permutation $i_1,\ldots,i_n$ of $1,\ldots,n$ such that all the $n$ adjacent sums $$i_1 + i_2,\ i_2 + i_3,\ \ldots,\ i_{n−1} + i_n,\ i_n + i_1$$ are prime.
In 2013 I made a similar conjecture involving twin primes. I conjectured that for any positive integer $n$ there is a circular permutation $i_0,i_1,\ldots,i_n$ of $0,1,\ldots,n$ such that all the $n + 1$ adjacent sums $$i_0 + i_1,\ i_1 + i_2, \ \ldots,\ i_{n−1} + i_n,\ i_n + i_0$$ belong to the set $$S=\{k ∈\mathbb N :\ 6k −1\ \text{and}\ 6k + 1\ \text{are twin primes}\}.$$ See http://oeis.org/A228917.
The construction in Douglas Zare's answer can be generalized to something that "heuristically" includes all sufficiently large even $N$, whether or not divisible by 3.
Suppose for some $p<N$ that both $p$ and $p+N$ are prime (or that $p=1$ and $N+1$ is prime). Then for $1\leq a,b \leq N$, the congruence $a+b\equiv p$ mod $N$ implies that $a+b$ is prime. This means that in the "prime-sum graph", the edges that connect numbers whose sum is congruent to $p$ mod $N$ constitute a perfect matching.
Suppose now that $q$ is another prime satisfying the same condition. Then we obtain two disjoint perfect matchings, and if we combine them to a set of 2-cycles, then the difference between numbers that are two steps apart (that is, consecutive odd or consecutive even numbers) will be congruent to (plus or minus depending on direction) $q-p$. It follows that the number of cycles is $\gcd((q-p)/2, N/2)$.
So if there are two such prime-pairs where the only common factor of $N$ and $q-p$ is 2, then the answer to the question of the hamiltonicity of the prime-sum graph is yes.
It is true that unless $N$ is divisible by 3, $p$ and $q$ will have to be either 3 or congruent to $N$ mod 3, so for some $N$, $q-p$ will always have a factor 3, but those $N$ aren't themselves divisible by 3, so the construction still works.
Of course, establishing the existence of such prime quadruples seems to be of "Goldbach level" of difficulty or even harder, but at least I had my computer check that they exist for all even $N$ up to $10^6$.