95

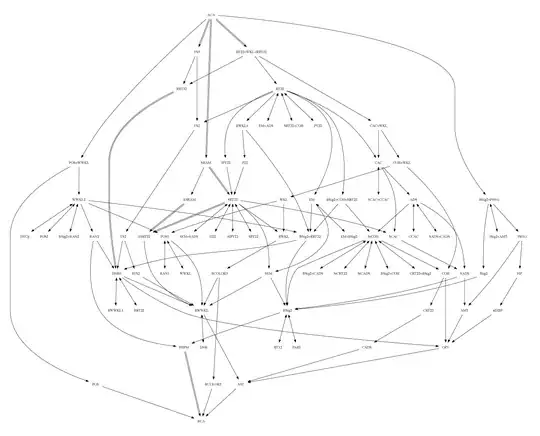
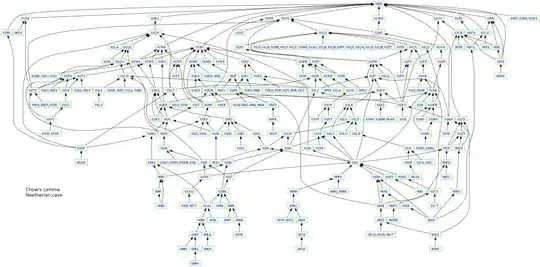
Given a proof for a result, one could denote the proof as a node on a graph, and then draw arrows to the node from axioms and previous results that the proof uses, and then draw arrows from the node to results that the result is used to prove. The sources of such a graph would be mathematical axioms and the sinks would be results which do not yet have corollaries. This is related to the facts that finite categories can be drawn as directed graphs and that proofs form a category.

Question: Is there an existing ontological/relational database somewhere that attempts to make use of such an idea to formally encode some of present-day mathematics?

It can often be difficult to fully trace all of the logical dependencies of a given result. For example, how can one show whether existing proofs of the Implicit Function Theorem use the Law of the Excluded Middle or not? Rather than spend a couple of days going through tens of textbooks and trying to parse their proofs, not for their content but just to see what assumptions they are using, wouldn't it be easier to ask a computer to do that task?

Such a system for tracking the logical dependencies of known proofs for existing theorems could be useful not only for beginners ("What important theorems use the completeness property of the real numbers? I'll check the database."), but it could also be useful for constructivists or intuitionists who want to keep track of which existing results make use of the Axiom of Choice or the Law of the Excluded Middle. And maybe it would be possible to use a sufficiently complete database to run tests to see whether the foundations of mathematics are consistent? I don't actually know, but it sounds on a naive level something that would be useful, even if it would take a long time to build.

Note: I am not sure what to tag this question or if it is on-topic.

Martin Sleziak
  • 4,608
Chill2Macht
  • 2,622
  • 7
    There is an earlier MO question that appears to be similar: http://mathoverflow.net/questions/208855/family-tree-of-theorems?rq=1 – Joe Silverman Sep 08 '16 at 19:14
  • 8
    It seems like it would be made tricky by the fact that theorems may have many different proofs. Suppose Theorem A has two known proofs, one from first principles and one which uses Theorem B. Theorem B also has two known proofs, one from first principles and one which uses Theorem A. How would you represent this without having a directed cycle in your graph? – Nate Eldredge Sep 08 '16 at 20:08
  • 1
    @JoeSilverman Yes I agree, the ideal would be to codify something like that mentioned in the question so it can be searched by computer – Chill2Macht Sep 08 '16 at 20:27
  • 3
    @NateEldredge I think the key would be to make each proof a separate node, and not the theorem itself. Then one could link together all proofs of the same theorem in another structure, for example by adding for each proof an outgoing edge to the node corresponding to the result which it proves. I'm not sure if the implementation would be better to make the result/theorem nodes sinks or not, but I think it might be good to have a bipartite structure -- arrows from "Proofs" enter "Thms" and arrows from "Thms" enter "Proofs", with no arrow going to a proof from a proof or to a reslt from a result – Chill2Macht Sep 08 '16 at 20:35
  • i.e. imagine that U is "Theorems" and "V" is proofs -- http://i.stack.imgur.com/KZ9eG.png – Chill2Macht Sep 08 '16 at 20:36
  • 4
    @NateEldredge I don't think directed cycles actually cause that much of a problem. Without directed cycles the algorithm for extracting the dependencies of a given theorem would be to recursively create a set containing all predecessors, predecessors of predecessors, etc. With directed cycles one can simply modify this algorithm by stipulating that no theorem can appear in its own dependency set. – Paul Siegel Sep 08 '16 at 20:54
  • 2
    Any two statements that are true are independent. One must define precisely what does “dependence of theorems” mean, since the number of different proofs for any theorem is unbounded. – Incnis Mrsi Sep 10 '16 at 17:37
  • 4
    An example that comes up on math.stackexchange is early in analysis when you want to define $e^x$. You can define $e^x=\lim_{n \to \infty}(1+\frac xn)^n$, you can define $e^x=\sum_{n=0}^\infty \frac{x^n}{n!}$, you can define $\log x = \int_1^x \frac 1y\ dy$ with $e^x$ the inverse function of $\log x$ and probably a few more. Once you choose one, the rest become theorems. Once we prove these theorems we lose track of which definition is at the root of the tree and regard all of them as established properties of $e^x$, available for use as required. What should be in the database for this? – Ross Millikan Sep 10 '16 at 23:34
  • 1
    @RossMillikan I think that just means that equivalent formulations lead to directed cycles, but isn't that to be expected? I mean the Axiom of Choice is equivalent to the well-ordering principle, you can choose either one and prove the other, if you're using both, without loss of generality you only assumed one of the two -- I don't see how this is or would be a problem. Same thing with supremum property of the real numbers and the intermediate value theorem, etc. – Chill2Macht Sep 10 '16 at 23:50
  • 1
    @IncnisMrsi There is an arrow from result A to result B if there exists (at least one) proof using result A to show result B is true. – Chill2Macht Sep 10 '16 at 23:50
  • 1
    But I think it makes it harder to think about the dependencies. If my definition of $e^x$ is the Taylor series and that is what I need for the proof at hand, I don't need any of those theorems. If my definition is the $\log x$ one, I need the theorem that the Taylor series is equivalent. I think you get forced to choose one specific set of axioms and definitions for your database, though there is disparity in the community on where to start. – Ross Millikan Sep 10 '16 at 23:58
  • 1
    @RossMillikan All of the proofs are valid, so all of the proofs should be in the database. Otherwise one has the false impression that the results and the possible definitions are not all equivalent, when they are. This is exactly the case with the implicit function theorem, the inverse function theorem, and the rank theorem, given one, the other two can be proved. Since they are equivalent, and hence essentially the same, what perhaps would be more meaningful would be to collapse the corresponding cycle into a single node, at least when attempting to understand the large scale structure. – Chill2Macht Sep 11 '16 at 06:52
  • 2
    Realms: A Structure for Consolidating Knowledge about Mathematical Theories presents an approach (geared toward formal systems) that addresses some of the concerns about multiple proofs of the same theorem and also different presentations of the same theory. – Derek Elkins left SE Sep 12 '16 at 10:55
  • 1
    Do you consider Metamath to meet the "present-day mathematics" criterion? I'm not sure whether you intend that to mean that you want a database of relationships between recent results, and if so what your cut-off for "recent" is. – Peter Taylor May 23 '18 at 12:01

5 Answers5

47

The reverse mathematics zoo, founded by Damir Dzhafarov and with recent development by Eric Astor, aims to be a database showing the relations and dependencies of mathematical theorems as described in the theory of reverse mathematics. An enormous number of the theorems of classical mathematics are now included in the reverse mathematical hierarchy, and appear in this database.

The system accepts new contributions, and is capable of generating diagrams showing the relations.

For example, the current results.txt file and the database is available in the rmzoo.zip file. There are various diagrams available http://rmzoo.math.uconn.edu/diagrams/, which are generated automatically from the database.

Pictured here is the Implications and Strict Implications diagram.

Reverse math implication diagram

Joel David Hamkins
  • 224,022
34

It's important to distinguish between two types of "dependencies."

The cleanest type of dependency is the kind that is studied in reverse mathematics: Theorem T depends on Axiom A if T is actually unprovable in the absence of A. Folks who study reverse mathematics make it their job to track dependencies of this type. Proof assistants such as Coq also allow you to track some such dependencies; for example, Coq doesn't have the law of the excluded middle built in, so you can definitively confirm (in some cases) that some theorem does not need the law of the excluded middle. So if this is the kind of dependency you're interested in, then there are people who are working hard on tracking it (but a complete database of the sort you're looking for isn't quite available yet).

There is another type of dependency that is less formal. An example might be "The only known proof of Theorem T relies on the classification of finite simple groups (CFSG)." We understand intuitively what this means, but it is difficult to formalize. CFSG is not an axiom, and we don't know any plausible way to formalize "a system of mathematics in which CFSG is unprovable but lots of other mathematics is provable." Thus the best we could do is to provide the computer with all known proofs and then it could verify that every known proof of T uses CFSG as a lemma. This is a much more ambitious task than formalizing at least one proof of every mathematical theorem, and even the latter project is at least decades away. For now, human expert knowledge is a better guide to this sort of thing than computers are.

Timothy Chow
  • 78,129
  • 1
    I would say this answers my question, because I had the latter type of dependency in mind. Why is "formalizing at least one proof of every mathematical theorem" "at least decades away"? Are people working on it at least? Would it be possible, today, to formalize one given book into such a system, say Baby Rudin for example? – Chill2Macht Sep 08 '16 at 20:53
  • 1
    @William see for instance https://www.isa-afp.org/topics.shtml for one such project. – András Salamon Sep 08 '16 at 22:08
  • @AndrásSalamon Thank you for the link -- I didn't even know this existed! Skimming over some of the pages it is now clearer to me why this is much more difficult than I previously thought – Chill2Macht Sep 09 '16 at 00:42
  • 4
    People in the formal theorem-proving community are working on it. One estimate I have heard is that it takes about one week (40 person-hours) to formalize a page of advanced mathematics. See for example Freek Wiedijk's slides here: http://www.cse.chalmers.se/research/group/logic/TypesSS05/Extra/wiedijk_sl.pdf The labor involved should decrease with time as people build better formalization tools, but until it is easy enough for all mathematicians to do it themselves, formalization will always lag well behind the published mathematical literature. – Timothy Chow Sep 09 '16 at 00:46
  • You formulated the “Theorem T depends on Axiom A if T is actually unprovable in the absence of A” condition ambiguously. Do you mean that, for certain class of theories, any theory obtaining T must have A as a theorem or an axiom? This indicates T ⇒ A — but it’s a “dependence” of reversed polarity, possibly equivalence (that is much stronger relation). Practically, if T ⇏ A, then we always can specially tailor such a set of axioms that T becomes a theorem while A doesn’t. – Incnis Mrsi Sep 11 '16 at 15:10
  • 1
    @IncnisMrsi : Rather than try to elaborate here, I think the best thing is for me to point you to the literature on reverse mathematics (which is so named precisely because of the "reversed polarity" that you noted). The standard textbook is Simpson's "Subsystems of Second-Order Arithmetic". And of course Wikipedia is a good entry point too. – Timothy Chow Sep 11 '16 at 18:27
  • Regarding my earlier comment about Baby Rudin, it seems that Wolfram Research recently did something similar with Munkres's Topology : http://blog.wolfram.com/2016/12/22/the-semantic-representation-of-pure-mathematics/ Normally I don't read the e-mails they send me but it seems like this time it was somewhat worthwhile. – Chill2Macht Jan 17 '17 at 10:32
21

The Stacks Project provides an example of what you're looking for. Every definition, lemma, theorem, etc. is given a tag, and the tags are used as references in proofs. They even provide an API for visualizing the tag graph using d3.js. Of course the scope of the project is limited to algebraic geometry and related topics, and I'm not sure whether or not they drill all the way down to axioms of set theory, but it's a pretty good start.

Paul Siegel
  • 28,772
18

Not an answer, just a diagram from the Stacks Project, mentioned by Paul Siegel, illustrating dependencies of "the results needed to prove Chow’s Lemma" (the Noetherian case):

     
ChowsLemSmall
          (Image from MathBabe blog.)
And here's a link to a larger image.
Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • Thank you so much! This is exactly the type of image I was hoping existed. I really appreciate it. – Chill2Macht Sep 09 '16 at 01:01
  • 6
    But note that the Stacks project is doing this for conceptual clarity. They do not attempt any logtical minimalism. Many of these dependencies would be easy to avoid logically, but were helpful to the exposition. – Colin McLarty Sep 09 '16 at 15:47
7

While the other answers given are quite good, there are a few other issues I would bring up.

(1) How do we avoid bogging the system down with irrelevant pieces of mathematics?

(2) Which axiomatic system do we use? If we use ZFC, there are in fact infinitely many axioms. Moreover, proving some well-known results can be quite messy when viewing things using the language of set theory, or even in some native theory. (For instance, look at how long it took to formalize the Feit-Thompson theorem in Coq!)

On the other hand, if we use multiple languages/axiomatic systems, we run into the fact that there are no sinks. For any axiom A in one system, there is another axiom B in another system, which can be proved equivalent using axioms from a third system! We then get into reverse mathematics, which is quite interesting, but also (rightly) limited to certain key theorems and their equivalences.

Pace Nielsen
  • 18,047
  • 4
  • 72
  • 133