32

It was proved by Kershner long ago that the thinnest (least density) covering of the plane by congruent disks can be obtained by enlarging the radii of the optimal circle packing to just cover the gaps in that packing:

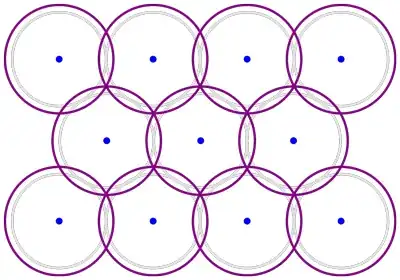
          CoverDisks
My question is:

Q. Is it known that, in the dimensions for which the optimal sphere packing is known $(2, 3, 8, 24)$, is it also known that a thinnest ball covering can be achieved by enlarging the spheres to just cover the interstices in the packing?

For example, now that the Kepler problem has been settled by Hales, does it follow that a thinnest ball packing of $\mathbb{R}^3$ can be obtained from the cannonball packing by enlarging the spheres to just cover the gaps?

          CoverBalls

Kershner, Richard. "The number of circles covering a set." American Journal of Mathematics 61.3 (1939): 665-671.

Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933

1 Answers1

34

Nope, this is false in three dimensions (where the body-centered cubic beats the face-centered cubic for covering) and eight dimensions (where $E_8$ is not even locally optimal). The Leech lattice is locally optimal and may be the best covering in twenty-four dimensions, but that would be a special fact rather than an instance of a general pattern. Overall sphere covering is more complicated than sphere packing, and there seems to be no close relationship between the optimal solutions.

Henry Cohn
  • 16,553
  • Thank you for the knowledgeable (and surprising) answer! – Joseph O'Rourke Oct 07 '16 at 20:54
  • 2
    Schuermann and Vallentin wrote several fascinating papers on the covering problem about a decade ago, including the one I linked to in the answer. I'm still amazed that $E_8$ isn't locally optimal, and it makes me wary of trying to intuit the answers to high-dimensional optimization problems. – Henry Cohn Oct 07 '16 at 22:07