Is it true that $X\times I\sim Y\times I\implies X\sim Y$?

Question

So I asked this question a few weeks ago on MSE and I was suggested to repost it here.

Let $I$ be the unit interval. Suppose that $X$ and $Y$ are topological spaces such that $X\times I$ is homeomorphic to $Y\times I$. Does it follow that $X$ is homeomorphic to $Y$?

As pointed out in the comments in the other thread, there are counterexamples to analogous questions with $I$ replaced by the circle or the real line. Therefore I expect the answer to my question to be negative too. I would be also interested in what one can assume about $X$ and $Y$ to make the implication true.

@IgorBelegradek: Ah, you are right. I was mis-remembering that. I have now deleted the comment, since it wasn't useful. You should leave yours in because it points to correct answers. — Robert Bryant, Jan 30 '17 at 22:35
The answer in http://mathoverflow.net/questions/26385/when-factors-may-be-cancelled-in-homeomorphic-products gives an example. — Igor Belegradek, Jan 30 '17 at 22:39

Wlodek Kuperberg · Accepted Answer · 2017-01-30T23:55:34.413

25

There are indeed counterexamples to which Igor Belegradek gave reference. Here is another counterexample in the plane, perhaps the simplest there is: Let $X$ be an annulus with one arc attached to one of its boundary components and another arc attached to the other boundary component, and $Y$ - an annulus with two disjoint arcs attached to the same one of its boundary components.

edited Jan 30 '17 at 23:55

answered Jan 30 '17 at 23:28

Wlodek Kuperberg

7,256

1

Nice example and picture. And that works as well with $I$ replaced by the half-line. – Joël Jan 31 '17 at 03:30
@Joël, I fully agree with your first sentence while I have doubts about your second sentence of your comment. – Włodzimierz Holsztyński Jan 31 '17 at 06:57
1

Really? Then my intuition must be wrong. I'll think more. – Joël Jan 31 '17 at 16:20
1

Oh yes, I see where I was wrong. In fact I don't know if $X \times I$ and $Y \times I$ are homeomorphic if $I$ is a half-line. – Joël Jan 31 '17 at 16:22
2

@Joël, actually, spaces $\ X\times[0;\infty]\ $ and $\ Y\times[0;\infty]\ $ are not homeomorphic. I am confident that I've proved it--for Wlodek K's example as well as for mine, for both. It'd be awkward to present my proof in a comment (while the thread seems to be closed, and further answer are not allowed). – Włodzimierz Holsztyński Jan 31 '17 at 20:13
2

Let me at least provide the first step (the easiest one but crucial): consider spaces $\ X'\ $ and $\ Y'\ $ obtained from $\ X\times[0;\infty)\ $ and $\ Y\times[0;\infty)\ $ respectively, by removing from them the points which are the centers of 3-dim balls contained in those Cartesian products. – Włodzimierz Holsztyński Jan 31 '17 at 20:19
2

This showed up in the Saint Petersburg Topology olympiad, I wonder if this was the reference http://mathcenter.spb.ru/nikaan/olympiad/problemseng.pdf – Andres Mejia Nov 30 '17 at 19:53

score 7 · Answer 2 · edited Aug 04 '21 at 05:55

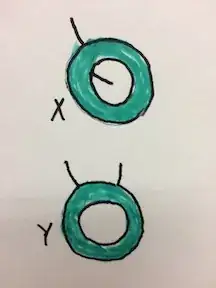
@WlodekKuperberg (perhaps) and I (for sure) were exposed to this kind of examples by Karol Borsuk, or possibly Karol Borsuk simply had an example like the one I will present below:

\begin{equation} D\ :=\ \{z\in\mathbb C: |z|\le 1\}\ \subseteq\ \mathbb C \ \end{equation} \begin{equation} A\,\ :=\,\ D\times\{0\}\ \cup\ \{1\ \ \ i\ \ -\!1\ \ -\!i\}\times [-1;0]\,\ \subseteq\,\ \mathbb C\times\mathbb R \end{equation} \begin{equation} X\,\ :=\,\ A\,\ \cup\,\ \{-1\ \ 1\}\times [0;1]\,\ \subseteq\,\ \mathbb C\times\mathbb R \end{equation} \begin{equation} Y\,\ :=\,\ A\,\ \cup\,\ \{i\ \ \ 1\}\times [0;1]\,\ \subseteq\,\ \mathbb C\times\mathbb R \end{equation}

Then $\ X\ $ and $\ Y\ $ are not homeomorphic while $\ X\times I\ $ and $\ Y\times I\ $ are.

REMARK One may check Karol Borsuk's series of publications about the uniqueness of topological decomposition into Cartesian products, and a paper by Hanna Patkowska about the uniqueness of the decomposition of ANRs into 1-dimensional ANRs.

A kind request (I'd greatly appreciate): Wlodek Kuperberg, please add a picture to my analytic description; let the pictures of $\ X\ $ and $\ Y\ $ be embedded into $\ \mathbb C;\ $ I mean homeomorphic copies of $\ X\ $ and $\ Y$.

ACKNOWLEDGEMENT I am grateful to Wlodek Kuperberg for providing such a very nice graphics (so cute and psychologically loaded; it's the first graphics illustration in my MO posts)). *** Włodek, congratulation on your another NICE answer (Gauss said, a few but ripe).

"$X$ and $Y$ are homeomorphic while $X\times I$ and $Y\times I$ are not"? — Jochen Wengenroth, Jan 31 '17 at 08:07
The other way around (of course). I'll fix it in a moment. ... Yes, done. — Włodzimierz Holsztyński, Jan 31 '17 at 09:28
@WłodzimierzHolsztyński: Kind request granted with pleasure :) — Wlodek Kuperberg, Jan 31 '17 at 15:27
@WłodzimierzHolsztyński: And yes, Wlodek, I remember this kind of examples, and many other as well, from the good old years of studying at Warsaw University, where Karol Borsuk exposed us to the world of topology of a wonderful geometric flavor. He was a true Master, and the kindest gentleman among gentlemen. — Wlodek Kuperberg, Jan 31 '17 at 17:12

Is it true that $X\times I\sim Y\times I\implies X\sim Y$?

2 Answers2