29

In general, we might ask when we can find interesting spaces $X, Y$ such that $X$ is homeomorphic to $[X, Y]$. By the Lawvere fixed point theorem $Y$ must have the fixed point property. Happily, $Y = [0, 1]$ does in fact have the fixed point property (e.g. by the intermediate value theorem), so this is not an obstruction.

I know that computer scientists have constructed spaces $X$ such that $X$ is homeomorphic to $X^X$ in domain theory, but I don't know enough about it to tell whether the techniques are relevant here.

Qiaochu Yuan
  • 114,941
  • 1
    Functions = continuous functions, I assume? – Igor Rivin Mar 17 '17 at 02:06
  • Yes, I suppose that's worth clarifying. Edited. – Qiaochu Yuan Mar 17 '17 at 02:36
  • 1
    I guess you are considering the compact open topology on $[X,Y]$? Or is the question is also about finding the topology on $[X,Y]$? – Cusp Mar 17 '17 at 05:20
  • Yes, the compact open topology. If I'm allowed to pick the topology on $[X, Y]$ then lots of silly things could happen, I imagine. – Qiaochu Yuan Mar 17 '17 at 05:22
  • 3
    There are two candidates one might consider as a first approximation: the direct limit of $C^k(I)\to C^{k+2}(I)\to C^{k+4}(I)\to...$ or the inverse limit of $...\to C^{k+4}(I)\to C^{k+2}(I)\to C^k(I)$ (the latter is $C(_)$ of the former) – მამუკა ჯიბლაძე Mar 17 '17 at 05:52
  • 3
    I'd pause before decreeing it should be the compact-open topology; I'd say it should be the exponential topology first and foremost, i.e., the topological structure such that there is a natural isomorphism $Top(-, [X, Y]) \cong Top(- \times X, Y)$. This need not be the compact-open topology (although it will be if $X$ is say locally compact Hausdorff). – Todd Trimble Mar 17 '17 at 12:18
  • Oh, interesting. For some reason I was under the impression that either the exponential topology agreed with the compact-open topology or the exponential didn't exist. In that case I of course want the exponential topology. – Qiaochu Yuan Mar 17 '17 at 22:37

1 Answers1

33

There cannot be such a homeomorphism, because Lawvere's fixed point theorem would give us something too constructive: a continuous map $[0,1]^{[0,1]} \to [0,1]$ that assigns a fixed point to each continuous map $[0,1] \to [0,1]$.

Following the proof of the Lawvere fixed point theorem, given a homeomorphism $f: X \cong [0,1]^X$ and a map $g: [0,1] \to [0,1]$, we construct a map $h: X \to [0,1]$ by $h(x) = g(f(x)(x))$, and then we get an element $x^* = f^{-1}(h)$ of $X$. Then,

$$ f(x^*)(x^*) = h(x^*) = g(f(x^*)(x^*)), $$

so we have found a fixed point of $g$. This construction is continuous in $g$, since we're working with the exponential topology on $[0,1]^{[0,1]}$, so $g \mapsto f(x^*)(x^*)$ gives a continuous fixed-point-finding map $[0,1]^{[0,1]} \to [0,1]$.

There is a lot of work on the nonconstructivity of Brouwer's fixed point theorem for different senses of constructivity. To give a quick visual proof that no continuous map of the type considered here exists, it is sufficient to consider a path through $[0,1]^{[0,1]}$ along which such a map cannot be continuously defined. Consider linearly deforming green to red to purple in the below diagram; a fixed point (i.e. a point where the curve crosses the identity depicted in blue) cannot be continuously chosen.

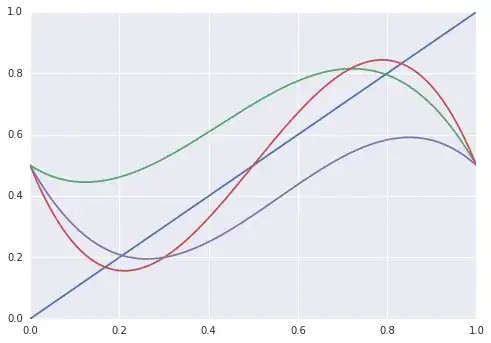
Three curves showing Brouwer is nonconstructive

It's interesting that this works because we have a homeomorphism $X \cong [0,1]^X$ rather than just a continuous surjection. A continuous surjection $X \to [0,1]^X$ would be enough to deduce the intermediate value theorem using Lawvere's fixed point theorem, but not in a constructive enough way to similarly rule out.

Sam Eisenstat
  • 546
  • Aha, nice construction! – Qiaochu Yuan Mar 22 '17 at 08:08
  • 4
    In fact for this argument to work, we don't need that $[0, 1]^X$ is homeomorphic to $X$, just that it is a retract of $X$. This observation is put to use in an answer on the related thread, here: https://mathoverflow.net/a/267603/2926 – Todd Trimble Apr 19 '17 at 12:07