Is the series $\sum_n|\sin n|^n/n$ convergent?

Question

Problem. Is the series $$\sum_{n=1}^\infty\frac{|\sin(n)|^n}n$$convergent?

(The problem was posed on 22.06.2017 by Ph D students of H.Steinhaus Center of Wroclaw Polytechnica. The promised prize for solution is "butelka miodu pitnego", see page 37 of Volume 1 of the Lviv Scottish Book. To get the prize, write to the e-mail: hsc@pwr.edu.pl).

This touches on research-level mathematics, but given the specific nature of the problem it seems like it might do better on math.SE rather than on mathoverflow. — Steven Stadnicki, Sep 28 '17 at 18:45
@StevenStadnicki Maybe, but this problem is not a standard university level exercise in Calculus. Moreover neither positive nor negative answers are not evident. Just try to resolve it yourself. It does not seem to be trivial. — Lviv Scottish Book, Sep 28 '17 at 18:50
Can anyone write a program and calculate the sequence of partial sums of this series? Does it seem to be bounded or not? Maybe $|\sin n|^n$ tend to zero? — Lviv Scottish Book, Sep 28 '17 at 18:58
@LvivScottishBook Partial sums won't do you any good in this case; the core question is whether $n$ can be close enough often enough to $(k+\frac12)\pi$ to 'disrupt convergence'. This is coupled closely to the irrationality measure of $\pi$, but I don't think too strong of a result is actually needed here. — Steven Stadnicki, Sep 28 '17 at 19:58
@LvivScottishBook: $|\sin n|^n$ does not tend to $0$ (this follows from the argument given in the answer here: https://math.stackexchange.com/questions/1141045/does-sum-n-1-infty-sin-ncn-converge-what-about-the-terms). — Will Brian, Sep 28 '17 at 20:01
@WillBrian: In that post, it is not obvious to me why $q$ can be chosen to be odd. — GH from MO, Sep 28 '17 at 21:12
A quick-and-dirty guess based on approximation of $|\sin(n)|$ by $|\sin(X_n)|$ with $X_n$ i.i.d. uniform on $[0,2\pi]$ suggests convergence: $\mathbb{E} |\sin(X_n)|^n \approx (2 /(\pi n))^{1/2}$. — Mateusz Kwaśnicki, Sep 28 '17 at 21:51
And after a while I think my previous comment can be made rigorous: $n \bmod \pi$ is roughly uniformly distributed over $[0,\pi]$ when $n \in {2^k, 2^k+1, \ldots, 2^{k+1}-1}$, and we have good bounds on how uniform it is. Combining this with $|\sin(n)|^n \leqslant |\sin(n)|^{2^k}$ and $1/n \leqslant 1/2^k$ for this range of $n$ should produce a rigorous proof. — Mateusz Kwaśnicki, Sep 28 '17 at 21:58
@GHfromMO I got curious about that (in a different but related context) a while ago: https://mathoverflow.net/questions/171457/can-we-get-good-rational-approximations-in-all-residue-classes/171729#171729 (spoilers - you can in fact choose q odd without disrupting the argument) — Steven Stadnicki, Sep 28 '17 at 22:43
@MateuszKwaśnicki: I am not sure we really have good bounds on the asymptotically uniform distribution of $n\bmod\pi$. Please tell us about results in this direction, I would be interested. — GH from MO, Sep 29 '17 at 00:38
@GHfromMO: That's not obvious to me either -- thanks for pointing out the hole in that argument. It looks like Steven Stadnicki's linked answer patches the hole, though, so it is true that $|\sin n|^n$ does not tend to $0$. — Will Brian, Sep 29 '17 at 02:07
@GHfromMO: Terry Tao's answer contains the details, so this is no longer relevant; anyway, what I meant is a bound on convergence in the ergodic theorem for irrational rotations with non-Liouville angle of rotation. I do not remember where I originally read about it; it is written explicitly in this paper as Theorem 2. According to the authors, it was first observed by Kakutani and Petersen in 1981 (see Appendix A in the linked paper). — Mateusz Kwaśnicki, Sep 29 '17 at 07:06
It almost assuredly would not have done better at Math.SE. It seems to have been a real test of professional skill and knowledge. — Todd Trimble, Sep 30 '17 at 16:32

Terry Tao · Accepted Answer · 2017-09-30T16:21:21.640

Note that if $\pi$ were rational (with even numerator), then $\sin(n)$ would equal $1$ periodically, so the series would diverge. Similarly if $\pi$ were a sufficiently strong Liouville number. Thus, to establish convergence, one must use some quantitative measure of the irrationality of $\pi$.

It is known that the irrationality measure $\mu$ of $\pi$ is finite (indeed, the current best bound is $\mu \leq 7.60630853$). Thus, one has a lower bound $$ | \pi - \frac{p}{q} | \gg \frac{1}{q^{\mu+\varepsilon}}$$ for all $p,q$ and any fixed $\varepsilon>0$. This implies that $$ \mathrm{dist}( p/\pi, \mathbf{Z}) \gg \frac{1}{p^{\mu-1+\varepsilon}},$$ for all large $p$ (apply the previous bound with $q$ the nearest integer to $p/\pi$, multiply by $q/\pi$, and note that $q$ is comparable to $p$). In particular, if $I \subset {\bf R}/{\bf Z}$ is an arc of length $0 < \delta < 1$, the set of $n$ for which $n/\pi \hbox{ mod } 1 \in I$ is $\gg \delta^{-1/(\mu-1+\varepsilon)}$-separated. This implies, for any natural number $k$, that the number of $n$ in $[2^k,2^{k+1}]$ such that $|\sin(n)|$ lies in any given interval $J$ of length $2^{-k}$ (which forces $n/\pi \hbox{ mod } 1$ to lie in the union of at most two intervals of length at most $O(2^{-k/2})$) is at most $\ll 2^{k(1 - \frac{1}{2(\mu-1+\varepsilon)})}$, the key point being that this is a "power saving" over the trivial bound of $2^k$. Noting (from Taylor expansion) that $|\sin(n)|^n \ll \exp( - j)$ if $n \in [2^k,2^{k+1}]$ and $|\sin(n)| \in [1 - \frac{j+1}{2^k}, 1-\frac{j}{2^k}]$, we conclude on summing in $j$ that $$ \sum_{2^k \leq n < 2^{k+1}} |\sin(n)|^n \ll 2^{k(1 - \frac{1}{2(\mu-1+\varepsilon)})}$$ and hence $$ \sum_{2^k \leq n < 2^{k+1}} \frac{|\sin(n)|^n}{n} \ll 2^{- k\frac{1}{2(\mu-1+\varepsilon)}}.$$ The geometric series on the RHS is summable in $k$, so the series $\sum_{n=1}^\infty \frac{|\sin(n)|^n}{n}$ is convergent. (In fact the argument also shows the stronger claim that $\sum_{n=1}^\infty \frac{|\sin(n)|^n}{n^{1-\frac{1}{2(\mu-1+\varepsilon)}}}$ is convergent for any $\varepsilon>0$.)

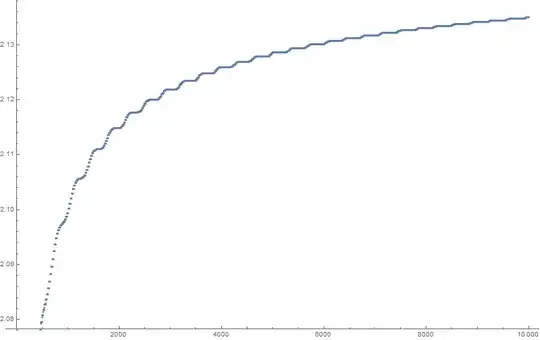
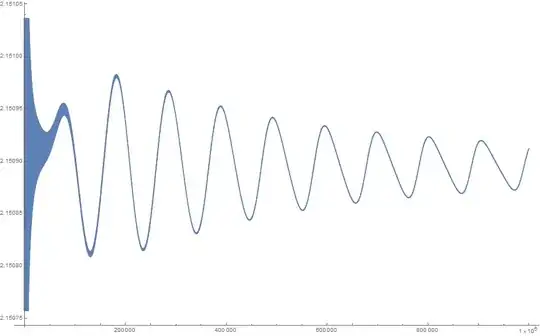
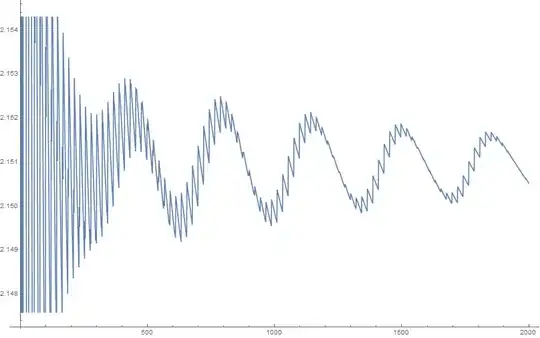
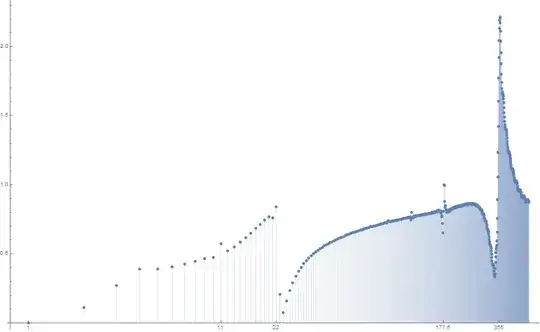
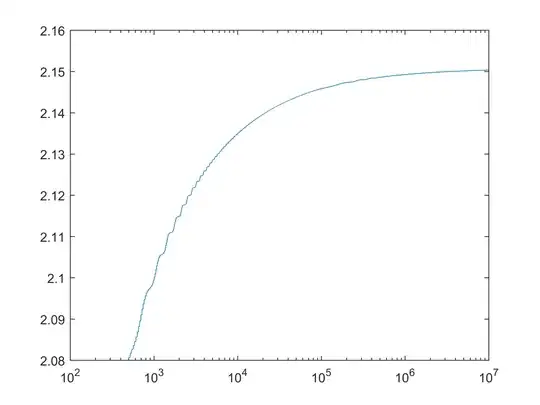
EDIT: the apparent numerical divergence of the series may possibly be due to the reasonably good rational approximation $\pi \approx 22/7$, which is causing $|\sin(n)|$ to be close to $1$ for $n$ that are reasonably small odd multiples of $11$. UPDATE: I now agree with Will that it is the growth of $-2^{3/2}/\pi^{1/2} n^{1/2}$, rather than any rational approximant to $1/\pi$, which was responsible for the apparent numerical divergence at medium values of $n$, as is made clear by the updated numerics on another answer to this question.

Will you be claiming the bottle of mead? (with an assist from google translate) — Anthony Quas, Sep 29 '17 at 05:05
Awesome! I wonder if also these very low frequency fluctuations clearly visible on Steve Huntsman's plot (especially in between $10^5$ and $10^6$) can be explained? — მამუკა ჯიბლაძე, Sep 29 '17 at 05:33
@TerryTao Great Solution! I have written to the Ph D students of Steinhaus Center about your solution of their problem. So, be ready to get the prize "butela miodu pitnego" (= a bottle of drinking honey :) — Lviv Scottish Book, Sep 29 '17 at 07:32
I don't think this 22/7 approximation is the culprit. The most suspicious region on მამუკა ჯიბლაძე's plot is for n>3000, elsewhere it looks highly convex. But $( (1/\pi) - (7/22) ) * 3000 = .3842\dots$ is quite large. Instead I think this is just the phenomenon of $1/\sqrt{n}$ going to zero pretty slowly and thus the graph continually increasing. — Will Sawin, Sep 29 '17 at 08:35
@WillSawin I am one deceived witness of that - the plot of $-1/\sqrt n$ looks pretty similar. On the other hand, the approximation $355/113$ is so good that odd multiples of $176$ and of $177$ might also be relevant. — მამუკა ჯიბლაძე, Sep 29 '17 at 09:50
I think the $2$ in the power of $n$ in the denominator can be removed. That is $\sum \frac{|\sin n|^n}{n^r}$ converges where $r>\max\left{\frac12, 1-\frac1{\mu-1} \right}$. — Sungjin Kim, Nov 08 '17 at 22:37
@AnthonyQuas It took a while, but I have indeed managed to claim the bottle of mead. https://mathstodon.xyz/@tao/110858903422243734 — Terry Tao, Aug 11 '23 at 06:16
$\mu\le7{.}103205334137\dots$ by https://arxiv.org/abs/1912.06345 — Emil Jeřábek, Aug 11 '23 at 11:30

მამუკა ჯიბლაძე · Answer 2 · 2017-09-30T21:06:52.733

40

On the OP request, here is the plot of first 10000 partial sums.

Following Terry Tao's suggestion, here is the plot of ($n$th partial sum) $+2^{\frac32}/\sqrt{\pi n}$ for $n$ up to one million:

The thick line in the beginning actually consists of high frequency oscillations - in the range up to 2000 it looks like this:

(I hope there are no rounding artifacts, I calculated everything with 100 decimal digits precision)

Next, following suggestion by j.c. in a comment below, I tried to plot the (discrete) Fourier transform of the first 10000 points; the result is this:

More precisely, height at the point with abscissa $n$ is the absolute value of the scalar product of the vector of first 10000 partial sums minus its average with the vector $\left(e^{\frac{2\pi i k}n}\right)_{1\le k\le 10000}$.

You see that $22$ and $355$, as well as $11$ ($=\frac{22}2$) and $177.5=\frac{355}2$ are all clearly visible.

If I will have more time I will try to do the same with more data, to detect $52163$ mentioned by Terry Tao in a previous comment. I am not sure about the arbitrary phase shift that I introduced, though - I could start with $k=0$ instead of $k=1$, or any other $k$.

edited Sep 30 '17 at 21:06

answered Sep 28 '17 at 20:59

მამუკა ჯიბლაძე

17,468

5

If you look at the random model, following Mateusz's calculations, the sum should grow like constant minus $2^{3/2} / (\pi n)^{1/2}$, which from 1000 to 10000 is a growth of .034, only slightly less then what you see. – Will Sawin Sep 29 '17 at 08:27
@WillSawin Yes I agree - actually I am convinced by Terry Tao's answer (at least up to details that I am able to understand), my post was before it. – მამუკა ჯიბლაძე Sep 29 '17 at 08:31
I'm saying that even without looking at Terry Tao's answer, you should not have found this graph very convincing. – Will Sawin Sep 29 '17 at 08:48
@WillSawin Well to be honest I was even more convinced after seeing Steve Huntsman's graph - it seemed hard to imagine it would ever stabilize. But now I looked at the graph of $-n^{-\frac12}$, and it leaves the same impression, so it is indeed very deceptive. – მამუკა ჯიბლაძე Sep 29 '17 at 09:20
5

Perhaps it is worth plotting the sum of the partial sums and $2^{3/2}/(\pi n)^{1/2}$, which should bring any deviations from the random model into clearer view, in particular the oscillations that are presumably coming from the rational approximants to pi. – Terry Tao Sep 29 '17 at 16:48
@TerryTao Many thanks, this way convergence is perfectly apparent. – მამუკა ჯიბლაძე Sep 29 '17 at 17:52
5

The low frequency oscillations may be related to the approximation $\pi \approx 52163/16604$, which makes $|\sin(n)|$ approximately periodic with period $52163$. – Terry Tao Sep 29 '17 at 18:59
10

Three years ago on Math.SE Jack D'Aurizio gave the estimate of $\leq 2.151$. See Is $ \sum\limits_{n=1}^\infty \frac{|\sin n|^n}n$ convergent？. – jeq Sep 30 '17 at 01:08
1

Here's yet another plotting suggestion: presumably we will see peaks corresponding to rational approximants of $\pi$ in the Fourier transform of the data (with the $2^{3/2}/(\pi n)^{1/2}$ adjustment). – j.c. Sep 30 '17 at 16:32
@j.c. Thank you, this is certainly sensible. My result is a bit messy but looks interesting - I wonder if there exist general methods to translate rational approximations into such kinds of plots... – მამუკა ჯიბლაძე Sep 30 '17 at 18:44
Cool! I'm used to seeing Fourier transform plots with the frequency (in your notation $2\pi/n$) on the x-axis and the amplitude (modulus of your computed points) or phase (argument) on the y-axis. The phase part will have some arbitrariness as you mentioned, so I'd be most interested in seeing the amplitude vs frequency plot. – j.c. Sep 30 '17 at 19:05
1

@j.c. I've changed it accordingly - indeed this is much easier to interpret. – მამუკა ჯიბლაძე Sep 30 '17 at 21:07

score 20 · Answer 3 · answered Sep 28 '17 at 21:22

20

Semilog plot building on მამუკა ჯიბლაძე's picture, this time to $10^7$

answered Sep 28 '17 at 21:22

Steve Huntsman

15,258

score 13 · Answer 4 · answered Nov 10 '17 at 23:47

Let $D_N$ be the discrepancy: $$ D_N=\sup \left| \frac{ A(J:P)}{N} - |J|\right| $$ where $P=\{k/\pi \ \mathrm{mod} \ 1\}_{k=1,2,\ldots, n}$, $J$ is an interval in $[0,1]$.

If the irrationality measure $\mu$ of $\pi$ is finite, then we have $$ D_N\ll N^{-\frac1{\mu-1} + \epsilon}. $$

From this result and Terry Tao's answer, the number of $n\in [2^k, 2^{k+1}]$ for which $|\sin n |$ falls in an interval of length $2^{-k}$, is $$ \ll 2^{\frac k2} + 2^{k\left(1-\frac1{\mu-1} + \epsilon\right)} $$

Thus, if $r>\max\left\{\frac12, 1-\frac1{\mu-1} \right\}$, then the series $$ \sum_{n=1}^{\infty} \frac{|\sin n|^n}{n^r} $$ is convergent.

It is conjectured that $\mu=2$. If we prove that $2\leq \mu <3$, then we can also prove that $$ \sum_{n=1}^{\infty} \frac{|\sin n|^n}{\sqrt n} $$ diverges. I am not aware of any unconditional proof of the divergence of this series.

Is the series $\sum_n|\sin n|^n/n$ convergent?

4 Answers4

Linked