Set theoretical multiverse and truths

Question

In J.D. Hamkins' multiverse view of set theory, every universe has an ill-founded $\mathbb{N}$ from the perspective of another universe. Does this mean that every proof in our universe can be seen as a nonstandard length proof from the perspective of some other universe, so that there is no real "truth" in the Multiverse?

Could this happen even for a simple concrete proof, like the fundamental theorem of arithmetic? Or are some some proofs standard-length in all universes?

Answer 1

Thank you for your interest in my views on the set-theoretic multiverse.

Yes, indeed, the well-foundedness mirage axiom you mention is probably the most controversial of my multiverse axioms, and so allow me to explain a little about it.

The axiom expresses in a strong way the idea that we don't actually have a foundationally robust absolute concept of the finite in mathematics. Specifically, the axiom asserts that every universe of set theory is ill-founded even in its natural numbers from the perspective of another, better universe. Thus, every set-theoretic background in which we might seek to undertake our mathematical activity is nonstandard with respect to another universe.

My intention in posing the axiom so provocatively was to point out what I believe is the unsatisfactory nature of our philosophical account of the finite.

You might be interested in the brief essay I wrote on the topic, A question for the mathematics oracle, published in the proceedings of the Singapore workshop on Infinity and Truth. For an interesting and entertaining interlude, the workshop organizers had requested that everyone at the workshop pose a specific question that might be asked of an all-knowing mathematical oracle, who would truthfully answer. My question was whether in mathematics we really do have a absolute concept of the finite.

To explain a bit more, the naive view of the natural numbers in mathematics is that they are the numbers, $0$, $1$, $2$, and so on. The natural numbers, with all the usual arithmetic structure, are taken by many to have a definite absolute nature; arithmetic truth assertions are taken to have a definite absolute nature, in comparison for example with the comparatively less sure footing of set-theoretic truth assertions.

To be sure, many mathematicians and philosophers have proposed a demarcation between arithmetic and analysis, where the claims of number theory and arithmetic are said to have a definite absolute nature, while the assertions of higher levels of set theory, beginning with claims about the set of sets of natural numbers, are less definite. Nik Weaver, for example, has suggested that classical logic is appropriate for the arithmetic realm and intuitionistic logic for the latter realm, and a similar position is advocated by Solomon Feferman and others.

But what exactly does this phrase, "and so on" really mean in the naive account of the finite? It seems truly to be doing all the work, and I find it basically inadequate to the task. The situation is more subtle and problematic than seems to me to be typically acknowledged. Why do people find their conception of the finite to be so clear and absolute? It seems hopelessly vague to me.

Of course, within the axiomatic system of ZFC or other systems, we have a clear definition of what it means to be finite. The issue is not that, but rather the extent to which these internal accounts of finiteness agree with the naive pre-reflective accounts of the finite as used in the meta-theory.

Some mathematicians point to the various categoricity arguments as an explanation of why it is meaningful to speak of the natural numbers as a definite mathematical structure. Dedekind proved, after all, that there is up to isomorphism only one model $\langle\mathbb{N},S,0\rangle$ of the second-order Peano axioms, where $0$ is not a successor, the successor function $S$ is one-to-one, and $\mathbb{N}$ is the unique subset of $\mathbb{N}$ containing $0$ and closed under successor.

But to my way of thinking, this categoricity argument merely pushes off the problem from arithmetic to set theory, basing the absoluteness of arithmetic on the absoluteness of the concept of an arbitrary set of natural numbers. But how does that give one any confidence?

We already know very well, after all, about failures of absoluteness in set theory. Different models of set theory can disagree about whether the continuum hypothesis holds, whether the axiom of choice holds, and so with innumerable examples of non-absoluteness. Different models of set theory can disagree on their natural number structures, and even when they agree on their natural numbers, they can still disagree on their theories of arithmetic truth (see Satisfaction is not absolute). So we know all about how mathematical truth assertions can seem to be non-absolute in set theory.

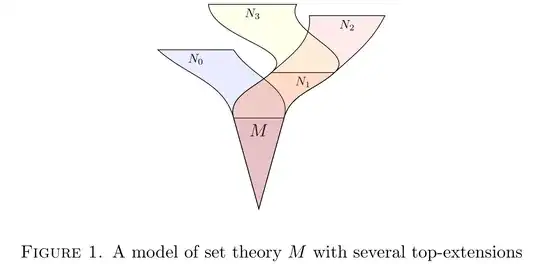
Skolem pointed out that there are models of set theory $M_1$, $M_2$ and $M_3$ with a set $A$ in common, such that $M_1$ thinks $A$ is finite; $M_2$ thinks $A$ is countably infinite and $M_3$ thinks $A$ is uncountable. For example, let $M_3$ be any countable model of set theory, and let $M_1$ be an ultrapower by a ultrafilter on $\mathbb{N}$ in $M_3$, and let $A$ be a nonstandard natural number of $M_1$. So $M_1$ thinks $A$ is finite, but $M_3$ thinks $A$ has size continuum. If $M_2$ is a forcing extension of $M_3$, we can arrange that $A$ is countably infinite in $M_2$.

No amount of set-theoretic information in our set-theoretic background could ever establish that our current conception of the natural numbers, whatever it is, is the truly standard one, since whatever we assert to be true is also true in some nonstandard models, whose natural numbers are not standard.

The well-foundedness mirage axiom asserts that this phenomenon is universal: all universes are wrong about well-foundedness.

In defense of the mirage axiom, let me point out that whatever attitude toward it one might harbor, nevertheless the axiom cannot be seen as incoherent or inconsistent, because Victoria Gitman and I have proved that all of my multiverse axioms are true in the multiverse consisting of the countable computably saturated models of ZFC. So the axiom is neither contradictory nor incoherent. See A natural model of the multiverse axioms.

I have discussed my multiverse views in several papers.

Hamkins, Joel David, The set-theoretic multiverse, Rev. Symb. Log. 5, No. 3, 416-449 (2012). Doi:10.1017/S1755020311000359, ZBL1260.03103.

<p><em>Hamkins, Joel David</em>, <a href="http://jdh.hamkins.org/multiverse-perspective-on-constructibility/" rel="noreferrer"><strong>A multiverse perspective on the axiom of constructibility</strong></a>, Chong, Chitat (ed.) et al., Infinity and truth. Based on talks given at the workshop, Singapore, July 25--29, 2011. Hackensack, NJ: World Scientific (ISBN 978-981-4571-03-6/hbk; 978-981-4571-05-0/ebook). Lecture Notes Series. Institute for Mathematical Sciences. National University of Singapore 25, 25-45 (2014). <a href="http://dx.doi.org/10.1142/9789814571043_0002" rel="noreferrer">DOI:10.1142/9789814571043_0002</a>,
 <a href="https://zbmath.org/?q=an:1321.03061" rel="noreferrer">ZBL1321.03061</a>.</p>

<p><em>Gitman, Victoria; Hamkins, Joel David</em>, <a href="http://jdh.hamkins.org/naturalmodelofmultiverseaxioms/" rel="noreferrer"><strong>A natural model of the multiverse axioms</strong></a>, Notre Dame J. Formal Logic 51, No. 4, 475-484 (2010). <a href="http://dx.doi.org/10.1215/00294527-2010-030" rel="noreferrer">DOI:10.1215/00294527-2010-030</a>, <a href="https://zbmath.org/?q=an:1214.03035" rel="noreferrer">ZBL1214.03035</a>.</p>

<p><em>Hamkins, Joel David; Yang, Ruizhi</em>, <a href="http://jdh.hamkins.org/satisfaction-is-not-absolute/" rel="noreferrer"><strong>Satisfaction is not absolute</strong></a>, to appear in the Review of Symbolic Logic.</p>

But finally, to address your specific question. Of course, there are specific finite numbers that will be finite with respect to any alternative set-theoretic background. As Michael Greinecker points out in the comments, the number 35253586543 has that value regardless of your meta-mathematical position. So of course, there are many proofs that are standard finite with respect to any of the alternative foundations.

Meanwhile, I find it very interesting to consider the situation where different foundational systems disagree on what is provable. In very recent work of mine, for example, we are looking at the theory of set-theoretic and arithmetic potentialism, where different foundational systems disagree on what is true or provable.

For example, recently with Hugh Woodin, I have proved that there is a universal finite set $\{x\mid\varphi(x)\}$, a set that ZFC proves is finite, and which is empty in any transitive model of set theory, but if the set is $y$ in some countable model of set theory $M$ and $z$ is any finite set in $M$ with $y\subset z$, then there is a top-extension of $M$ to a model $N$ inside of which the set is exactly $z$. The key to the proof is playing with the non-absolute nature of truth between $M$ and its various top-extensions.

Answer 2

There is a subtle issue here but it is not where the OP thinks it is. Any explicitly written integer is obviously "standard" whereas each new integer arising in the ultrapower of $\mathbb N$ is obviously "nonstandard". The subtle issue is that in the particular $\mathbb N$ we are working with, there may be integers (certainly bigger than the explicitly written ones) that look nonstandard from the viewpoint of another set-theoretic universe.

But this does not change the fact that any concrete proof has "standard" length. And since we are accepting ZFC axiomatics for each instance of a universe in Hamkins' multiverse, this has nothing to do with ultrafinitism.

In this publication (see also here) we proved a theorem that each universe in the Hamkins-Gitman "toy model" actually turns out to be a model of a variant of Edward Nelson's Internal Set Theory. Translated into the terms of Robinson's framework, this means that the integers in each instance of a universe in the multiverse contain not only an initial cut including all explicitly specifiable integers, but also a wealth of integers that are infinite according to a "smaller" universe in the multiverse.

One should note that the idea of a "standard $\mathbb N$" being an illusion, as implied in these question and answers, was the main driving force behind Petr Vopěnka's approach to the foundations of mathematics, formulated as his Alternative set theory already in the 1970s, according to what I have read of Vopenka's work.

Answer 3

I think only Joel can answer this question, but I'd like to point out that there are some subtleties here that the commenters are missing. In Joel's multiverse conception, there is no "standard" $\mathbb{N}$, so the standard natural numbers in one model could turn out to be nonstandard in another model. This means that something that appears to be a proof in PA in one model would be revealed to have nonstandard length, and not be a proof, in some other model.

So: "Length 35253586543 is always length 35253586543"? I'm not even sure we know, from Joel's perspective, that 35253586543 is a standard natural number in every model. It would take a long long time to actually count that high. Surely in models with nonstandard $\mathbb{N}$ it seems like nonstandard numbers are standard, and you could count up to them and think that you had executed only a finite number of steps. So how could you know that numbers you think are standard are also seen as standard by everyone else? Maybe for small numbers you can just directly intuit this, but this gets pretty philosophical.

You could argue that this number is only 11 digits long, and maybe we could give a proof that all 11 digit long numbers have to be standard in every universe, such that the proof itself was sufficiently short that we could just directly "see" that it continues to be a proof in any model. Maybe. That would at least require some serious argumentation.

"The actual proofs that we use have standard lengths" --- of course it would seem that way to us, but might our proof of the fundamental theorem of arithmetic turn out to have a nonstandard length in some other model? How could we know it wouldn't? You see these questions are a lot more subtle than they seem at first.

Edit: I guess I ought to clarify that I am NOT expressing my own view here. In my view, which is otherwise close to Joel's, there is a standard $\mathbb{N}$ and an absolute notion of arithmetical truth. However, there are no uncountable sets and "sets" like the real line are actually proper classes. So if ZFC is consistent then it has a range of countable models, but no canonical model.

I came to this view as a result of clarifying what I think is the essential difference between sets and proper classes (something philosophers of mathematics have struggled to explain). I have several papers on the arXiv which lay out my position; "Mathematical conceptualism" is probably the best place to start. The fullest account of my ideas about the set/proper class distinction is given in the last chapter of my book Truth & Assertibility.

Answer 4

Since the Fundamental Theorem of Arithmetic is a theorem of $PA$, it holds for both standard and nonstandard models of $PA$. Since one can interpret $PA$ in both $ZFC$ and $GBC$ (e.g., for $ZFC$, it is interpretable in $ZFC$ as the fragment $ZFC$ $-$ Infinity--note that in $ZFC$ all definitions of "finite" are equivalent, while in $ZF$ there are an "infinitude of finitudes" but since $V_{\omega}$ $\vDash$ $ZF$ $-$ Infinity also satisfies $ZFC$ $-$ Infinity, all definitions of 'finite' for $V_{\omega}$ are still equivalent), one can see that $PA$ is interpretable in some background set theory so as long as one's model of $PA$ can be interpreted in a model of $ZFC$ (say), then the Fundamental Theorem of Arithmetic will hold.

[Addendum: Though Andres is right, i.e., that interpretations are not theories, one can interpret one theory in another (see Richard Kaye's and Tin Lok Wong's paper, "On interpretations of arithmetic and set theory", for the interpretation of $PA$ in $ZF$ and $ZFC$). I am using this interpretation in order to show that, given the right background set theory ($ZFC$), one still has that the Fundamental Theorem of Arithmetic will hold in models of $ZFC$ for its interpretation of $PA$, regardless of whether the model of $PA$ in question is 'standard' or 'nonstandard' (whatever those terms might mean in Hamkins' set-theoretic multiverse).]