10

Let $X$ be a locally compact Hausdorff space. Call $X$ rigid if its only autohomeomorphism is the identity, $\operatorname{Homeo}(X)=\{1\}$.

Questions:

  1. Let $X$ be rigid. Is it true that every open subset $Y\subset X$ is rigid, i.e., $\operatorname{Homeo}(Y)=\{1\}$?

  2. Let $Y\subset X$ be open. Is it true that every autohomeomorphism of $Y$ extends (perhaps non-uniquely) to an autohomeomorphism of $X$?

  3. What can we assume about $X$ additionally to make sure that the answer to question 1 is positive? Metrizability, separability?

Discussion:

An affirmative answer to question 2 obviously implies an affirmative answer to question 1. Question 2 may be asking for too much, but there are simple cases where it is true. For instance, given a continuous bijective function $f:(0,1)\to(0,1)$, it can be continuously continued to a bijective function $F:\mathbb{R}\to\mathbb{R}$, hence every autohomeomorphism of $(0,1)$ can be continued to an autohomeomorphism of $\mathbb{R}$. A positive answer to question 1 seems more realistic to me. For instance, it is true for the Cook's curve, I believe. It is harder for me to check this condition for other examples of rigid spaces in the literature.

Thank you.

Jeremy Rickard
  • 33,905
Bedovlat
  • 1,939
  • 3
    I’m not very familiar with the Cook’s curve (call it $C$), but if $C’$ is the Cook’s curve with one point removed, then does the disjoint union $X=C\coprod C’$ work as a counterexample? It has an open subspace $C’\coprod C’$, which is clearly not rigid. – Jeremy Rickard Nov 06 '17 at 18:24
  • 2
    Just an example of some simple (non-rigid) space, where the second question has negative answer: consider a cylinder $S^1\times \mathbb{R}$. View $S^1$ as $\mathbb{R}\cup{\infty}$. The map $(x,y)\to (x,y+\arctan x) $ is a self-homeomorphism of $\mathbb{R}^2$, but cannot be extended to an automorphism of the cylinder, because when $x$ goes to $+\infty$ and $-\infty$ the limits do not match. – erz Nov 07 '17 at 03:39
  • 2
    If you remove the requirement that $X$ be locally compact, then (2) has a negative answer. Consider $X=\omega \cup {U,V}$ where U and V are R-K incomparable ultrafilters on $\omega$, equiped with the topology $P(\omega)\backslash(U\cup V) \cup { A \cup {U}: A\in U} \cup { B \cup {V}: B\in V}$ – Not Mike Nov 07 '17 at 05:37
  • In the context of the space $X$ from my last comment, $\omega$ is a decidedly non-rigid open subset. While $X$ itself is rigid. (PS: I meant to say the topology is generated by the collection of subsets given) – Not Mike Nov 07 '17 at 05:55
  • 1
    @Bedovlat Please see this answer as a related post https://mathoverflow.net/questions/198704/totally-non-fixed-point-property/198736#198736 – Ali Taghavi Nov 07 '17 at 11:06

3 Answers3

8

The answers to (1) and (2) are "no" in general for metrizable spaces.

Let $C$ be a connected compact metric space with more than one point, with the property that the only continuous self-maps of $C$ are constant maps and the identity. For example, Cook's curve has this property.

Let $C'$ be $C$ with one point removed. Since any autohomeomorphism of $C'$ extends to an autohomeomorphism of $C$ (its one-point compactification), $C'$ is also rigid.

Let $X$ be the disjoint union of $C$ and $C'$. Since $C$ is a connected component of $X$ and has no nonconstant continuous maps to $C'$, any autohomeomorphism $f$ of $X$ must satisfy $f(C)=C$ and hence $f(C')=C'$. Since both $C$ and $C'$ are rigid, $f$ is the identity, and hence $X$ is rigid.

But $X$ has the disjoint union of two copies of $C'$ as an open subspace, which is clearly not rigid, since there is an autohomeomorphism swapping the two copies.

Jeremy Rickard
  • 33,905
  • 2
    You've claimed to answer only (1) and (2), but you've also shown that the answer to (3) is "no" for the two properties specifically mentioned in the question, separability and metrizability. Great answer! Here is a reference for Cook's curve, which might be good to have here: http://matwbn.icm.edu.pl/ksiazki/fm/fm60/fm60123.pdf. – Will Brian Nov 07 '17 at 10:37
  • 2
    However, one more important property (which I did not explicitly mention in my question) we have not considered yet is connectedness of $X$. The non-existence of non-trivial clopen subsets makes life more difficult (or easier, depending on the perspective). – Bedovlat Nov 07 '17 at 12:12
  • 2
    @Bedovlat I believe you can get a connected example by taking a wedge sum $C\vee C'$ of $C$ and $C'$ instead of the disjoint union. I think that's still rigid, but it has an open subspace $C'\vee C'$. – Jeremy Rickard Nov 07 '17 at 14:38
  • Wedge sum involves identification of two points - one on each part, and the resulting topology is sensitive to the choice of those points. Maybe I am slow, but it isn't immediately clear to me which points you identify in $C$ and $C'$. – Bedovlat Nov 07 '17 at 23:24
  • @Bedovlat The same point. I.e., Pick $x,y\in C$ with $x\neq y$, let $C’=C\setminus{x}$, and take $C\vee C’$ identifying $y\in C$ with $y\in C’$. – Jeremy Rickard Nov 07 '17 at 23:29
  • I think, you have troubles if $y$ is such that $C\setminus{y}$ is disconnected. Then $C\vee C'$ is not rigid. Not sure if this happens with Cook's curve, though. I guess that Cook's curve is not like a simple curve, and it has at least one point $y$ which is not a bridge. But needs to be checked to be sure. Thanks a lot for this. – Bedovlat Nov 08 '17 at 11:39
  • 1
    $C\setminus{y}$ is connected. If it were the disjoint union of two non-empty open sets $A$ and $B$ then there would be a continuous self-map of $C$ that is the identity on $C\setminus A$ and the constant map to $y$ on $C\setminus B$, contradicting the fact that the only continuous self-maps of $C$ are the identity and constant maps. – Jeremy Rickard Nov 08 '17 at 13:02
  • There exists a fairly simple counterexample to the first question, even a locally connected, one-dimensional continuum non-separating the plane. (Cook's curves are not locally connected, but they possess a much stronger property than rigidity.) – Wlodek Kuperberg Nov 08 '17 at 22:30
  • Jeremy Rickard, agreed. And I guess $C\vee C\vee C$ identifying points $x,y\in C$, $x\neq y$, provides an example of a compact connected $X$. Wlodek Kuperberg, arguments used above involved not just rigidity but strong rigidity, i.e., that every continuous self-map is either identity or constant. If you know an argument that uses merely rigidity, I would appreciate an exposition. – Bedovlat Nov 08 '17 at 23:44
  • @Bedovlat, will do soon. Should I write it as an answer to your question? – Wlodek Kuperberg Nov 09 '17 at 20:06
  • Wlodek Kuperberg, please, do it your favourite way. You may post it as an answer, or send me a tex file by any means. I just want to understand the mechanism. Thanks. – Bedovlat Nov 09 '17 at 21:09
6

For the third question: If you assume that $X$ is zero-dimensional (i.e., it has a basis consisting of clopen sets), then the answer to question 1 is yes.

Proof: Suppose $U$ is an open, non-rigid subset of $X$, and let $h: U \rightarrow U$ witness its non-rigidity, so that $h(x) = y$ for some $x \neq y \in U$. Using zero-dimensionality, we can find a clopen subset $W$ of $U$ such that $h(W) \cap W = \emptyset$ (let $V_x, V_y$ be disjoint clopen sets containing $x$ and $y$, and let $W = V_x \cap h^{-1}(V_y)$). Then you can define a non-identity homeomorphisms $h': X \rightarrow X$ by taking $h' = h$ on $W$, $h' = h^{-1}$ on $h(W)$, and $h' = \mathrm{id}$ everywhere else.

For example, every rigid subset of the real line is zero-dimensional, so a subset of $\mathbb R$ is rigid if and only if each of its open subsets is.

Will Brian
  • 17,444
  • Thanks for this very instructive answer. Before accepting it as final, I will wait a little bit to see if someone comes up with a weaker sufficient condition. – Bedovlat Nov 07 '17 at 09:58
2

Here is a counterexample to the first question, a planar, non-separating one-dimensional locally connected continuum.

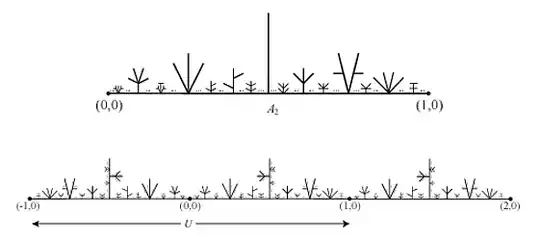
Let $A_1$ be the line segment in the $xy$-plane $\mathbb{R}^2$ with end points $(0,0)$ and $(1,0)$. Define set $A_2$ as the union of $A_1$ with a sequence of mutually disjoint trees (finite acyclic graphs) $T_i$, no two of them homeomorphic, each attached to $A_1$ at a single point other than the end point of $A_1$. The diameters of the trees should converge to zero, and the set of points of attachment should be dense in $A_1$ (see the first drawing). Also, $A_2\setminus A_1$ should be contained in the vertical open strip $0<y<1$. Observe now that every homeomorphism of $A_2$ onto itself must be the identity on $A_1$.

Next, to construct $A_3$, to each edge of every tree attached to $A_1$, attach a sequence of trees at a single point of the edge, in a similar manner as previously, and iterate this procedure, creating a nested sequence of sets $A_n$, each of which is a tree. Make sure that the diameters of the union $A=A_1\cup A_2\cup A_3\ldots$ is bounded, that the only points of $A$ lying on the boundary of the open strip $0<y<1$ are the end points of $A_1$. Also, make sure that the closure of $A$ (in $\mathbb{R}^2$), which we call $B$, does not contain any simple closed curve. This last requirement can be satisfied by designing the trees attached in the recursive procedure to be sufficiently small.

It is easy to see that every homeomorphism of $A_3$ onto itself must keep every point of $A_2$ fixed, and under any homeomorphism of $B$ onto itself, each point of $A_n$ must be fixed. Hence $B$ is rigid. Let $B’$ be the reflection of $B$ in the $y$-axis, let $X=B\cup(B’)\cup(B+(1,0))$, and let $U=[B\cup(B’)]\setminus\{(-1,0),(1,0)\}$ (see the second drawing). Here is the open set $U$, in the rigid space $X$, and it is not rigid, since it is symmetric about the $y$-axis.

Note 1. The set $B$ can also be described as the inverse limit of the nested sequence $\{A_n\}\ (n=1,2,\ldots)$ with the obvious retractions $r_n$ from $A_{n+1}$ to $A_n$, collapsing each tree in $A_{n+1}$ attached to $A_n$ to its point of attachment, as the bonding maps.

Note 2. In each stage of the construction a sequence of trees is used. In all, a countable number of trees appear; we may assume that all of them are mutually non-homeomorphic, though it is not quite necessary.

Wlodek Kuperberg
  • 7,256
  • Thanks a lot for the exposition, this is also very instructive. I need time to digest this. – Bedovlat Nov 11 '17 at 17:15
  • 1
    The rigidity of $B$ is easier to prove if in the construction all trees are topologically different. For instance, in the $n$-th recursive step, the trees attached are of the form: $n\times i$ segments emanating from a common end point, and each of them is attached to $A_{n-1}$ with that very point. – Wlodek Kuperberg Nov 11 '17 at 18:26
  • 1
    A crucial property of $B$ is its $unique$ arcwise connectivity: for every pair of distinct points, there is a unique arc joining them. – Wlodek Kuperberg Nov 11 '17 at 18:40
  • Correction: In my comment above, it should be $p_n\times 2^i$, where $p_n$ is the $n$-th prime, instead of $n\times i$. – Wlodek Kuperberg Nov 11 '17 at 23:20