Great mathematical figures and/or diagrams?

Question

Most math papers have few figures, if any, although sometimes a well-chosen figure can be a tremendous help in understanding mathematical concepts. Does anyone have any examples of notable uses of figures in mathematical writing and/or texts that make great use of figures/diagrams/illustrations?

Answer 1

Mumford's picture of Spec(Z[x]) comes to mind.

You can read a discussion of it here.

Answer 2

I am a huge fan of the drawings of Anatoly Fomenko (for some of his drawings, see here; for a description of his odd historical theories, see his wikipedia pages here and here).

In particular, his book "Algorithmic and Computer Methods for Three-Manifolds" with Matveev (which really has nothing to do with computers) is IMHO one of the best intro books on 3-manifolds available largely because of its drawings. The mathscinet review of the Russian version is worth reading; see

MR1162113 (93f:57002) Matveev, S. V.; Fomenko, A. T. {\cyr Algoritmicheskie i kompʹyuternye metody v trekhmernoĭ topologii}. (Russian) [Algorithmic and computer methods in three-dimensional topology] Moskov. Gos. Univ., Moscow, 1991. 303 pp. ISBN: 5-211-01743-9

EDIT : To give an idea of how amazingly cool the above book is, I have posted two pages of it here and here. It's a crying shame that it is not better known...

Answer 3

A paper that used figures to, in my view, revolutionize the understanding of an area of mathematics is: R. Penrose. Applications of negative dimensional tensors. In D.J.A. Welsh, editor, Combinatorial mathematics and its applications, pages 221–244. Mathematical Institute, Oxford, London, New York, Academic Press, 1971.

Answer 4

Turning a sphere inside out

http://www.treeincarnation.com/images/centerfold.gif

Answer 5

The book by G. K. Francis entitled "A topological picturebook" is beautiful. Have a look at this snapshot, starting with page 16.

The book explains how to draw and visualize pictures of low dimensional famous topological spaces: the dunce hat, a tetrahedral hyperbolic manifold, the Withney bottle, the Hopf fibration, and so on.

Answer 6

When I was an undergraduate I read the book Intuitive Topology by Prasolov. It's a wonderful illustrated guide to low-dimensional topology (mostly knots/links and surfaces). If I recall correctly, almost all of the "proofs" are by pictures.

Answer 7

Edward Tufte's books are quite beautiful, though they do not focus so much on mathematical figures/diagrams per se. However, via Tufte, I did come across this version of Euclid's Elements by Oliver Byrne, which presents the propositions and proofs of the Elements using colored diagrams and symbols. I'm not sure whether Byrne's edition is clearer or better to learn from than the original Euclid, but it sure is pleasing to look at.

Answer 8

Arnol'd was famous for his pictures (that poor $\ $ s-t-r-e-t-c-h-e-d $\ $ cat...), but the Award for Best Pictures must surely go to "Geometry and the Imagination" by D. Hilbert and S. Cohn-Vossen.

Answer 9

Reid's Undergraduate Commutative Algebra has a lot of great figures, most notably the frontispiece depicting the statement "let $A$ be a ring and $M$ an $A$-module" geometrically.

Answer 10

Geometry in Figures "written" by Arseniy Akopyan consist only of Figures. From Preface:

This book is a collection of theorems (or rather facts) of classical Euclidean geometry formulated in figures. The figures were drawn in such a way that the corresponding statements can be understood without any additional text.

Answer 11

The following is a wondeful candidate: Jos Leys, Lorenz and Modular Flows: A Visual Introduction, Feature Column of the AMS web site, November 2006.

Answer 12

Here's one of my favorite diagrams, based on a paper by Lawrence Leemis:

Probability distribution relationships

Also, here are some diagrams due to Robert Bartle relating various modes of convergence:

Diagramming modes of convergence

Answer 13

There's a chapter in Littlewood's "Mathematician's Miscellany" entitled The Zoo, which has many charming examples of pictoral proofs inspired by various animals.

Answer 14

In my opinion, a book that sets a new standard, not only in the quality of the pictures, but in overall design is A singular mathematical promenade by Étienne Ghys. A free PDF of the book is available here:

http://perso.ens-lyon.fr/ghys/promenade/

The pictures are in fact more vivid in the PDF version than on paper.

Answer 15

Knots, links, braids, and 3-manifolds, by Prasolov and Sossinsky (you can look at it on Google books) essentially has a picture on every page. They are very pretty.

Indra's pearls by Mumford, Series, and Wright has some breath-taking pictures. There are also cartoons by Gonick, which improves any book. Here's the copy at Google books.

Edit: A topological picturebook, by Francis is wonderfully illustrated. There are directions for reproducing the figures, as well as their mathematical meaning. Chapter eight of the book deals with the figure eight knot. :)

Answer 16

see my starting effort to help see 3-manifolds at http://commons.wikimedia.org/wiki/Category:3-manifolds

Answer 17

H.S.M. Coxeter's books include Regular Polytopes. This book deals with the classification of regular polytopes. In this book there are Coxeter diagrams which are closely related to Dynkin diagrams. In his works are many diagrams,figures and illustrations. They influenced M.C Escher. Many of Escher's works reflect his ideas. In 1996 Coxeter published a paper on one of these "Circle Limit III." For more information see here and here.

Answer 18

I like Cichon's diagram, which can be approximated in Mathjax better than almost any other entry on this list:

$\require{AMScd} \minCDarrowwidth13pt \begin{CD} @. \operatorname{cov}({\mathcal L}) @>>> \operatorname{non}({\mathcal B}) @>>> \operatorname{cof}({\mathcal B}) @>>> \operatorname{cof}({\mathcal L}) @>>> 2^{\aleph_0}\\ @. @AAA @AAA @AAA @AAA \\ @. \uparrow @. \mathfrak{b} @>>> \mathfrak{d} @. \uparrow \\ @. @AAA @AAA @AAA @AAA \\ \aleph_1 @>>> \operatorname{add}({\mathcal L}) @>>> \operatorname{add}({\mathcal B}) @>>> \operatorname{cov}({\mathcal B}) @>>> \operatorname{non}({\mathcal L}) @. \end{CD}$

(The triple arrows on the left and right should be long single arrows.)

All the entries are cardinal characteristics of the continuum, and the arrows mean $\le$.

Furthermore, the diagram describes all but two of the $\operatorname{ZFC}$-provable relations between those cardinalities: If $A$ is an assignment of the cardinals $\aleph_1$ and $\aleph_2$ to the ten cardinals in Cichoń's diagram, satisfying $$\operatorname{add}({\mathcal B})=\min\{\operatorname{cov}({\mathcal B}),{\mathfrak b}\}, \\ \operatorname{cof}({\mathcal B})=\max\{\operatorname{non}({\mathcal B}),{\mathfrak d}\}$$ and having no arrow in the diagram go from $\aleph_2$ to $\aleph_1$, then $A$ can be realized in some model of $\operatorname{ZFC}$.

Answer 19

The figures in John Stillwell's books are always superbly drawn, and really enhance the exposition.

Answer 20

Bar-Natan's first paper on Khovanov homology (On Khovanov's Categorification of the Jones Polynomial, Algebraic and Geometric Topology 2-16 (2002) 337-370) included a great figure (visible immediately if you follow this link) that summarised the entire construction. A great improvement over the previous epic, Khovanov's A categorification of the Jones polynomial.

Answer 21

The standard diagram for representing a category, showing objects, arrows/morphisms and the composition operation:

(source: Wikipedia/Wikimedia)

(The required identity arrows are elided here, which I find reasonable but which could easily be added without disturbing the diagram too much if their absence bothers you.)

Answer 22

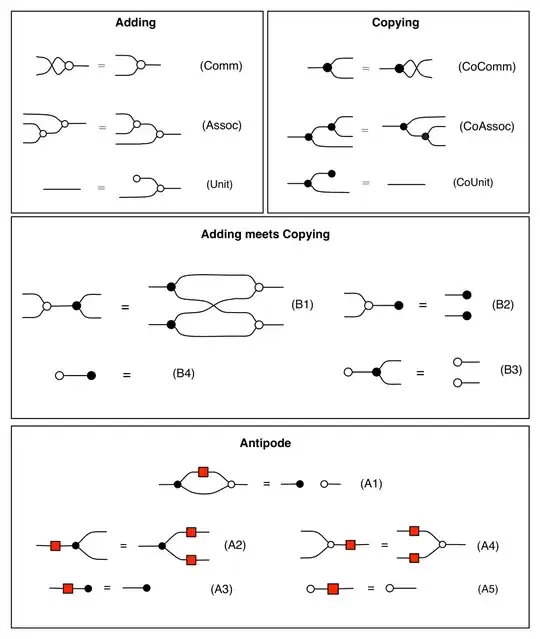
String diagrams are a very nice way to turn category-theoretic equations into beautiful pictures. Here are, for example, the axioms for (co)commutative Hopf algebras, which I find particularly satisfying in string diagram notation (taken from https://graphicallinearalgebra.net/).

Answer 23

There is the notion of a "proof without words" and a series (well, n=2) of books with that title.

https://en.wikipedia.org/wiki/Proof_without_words