6

(1) $\mathbb{R}^2$.

I'd like to place $n$ points in the plane so that the smallest angle they determine is as large as possible. In a sense, such a point set is in very general position, not only avoiding three points collinear, but also avoiding near collinearities.

Define the smallest angle of a set $S$ of points to the be smallest angle of any triangle formed by three points in $S$. So the $n=4$ and $n=5$ point sets shown below have smallest angles $45^\circ$ and $36^\circ$ respectively.

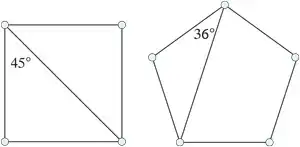
          PtsNoSmallAngs

Q1. What is the maximum of the smallest angle determined by any set $S$ of $n$ points, the maximum over all $S$? Is $S$ the vertices of a regular $n$-gon?

Update. Answered Yes by fedja with a nice proof in the comments.

(2) $\mathbb{R}^3$ (Added).

In 3D, the optimal arrangement seems to be akin to packing points on a sphere, e.g., the Tammes problem or the Thompson problem. Below shows the smallest angle realized by the $12$ vertices of the icosahedron.

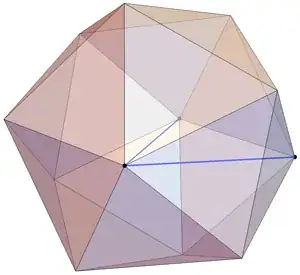
          IcosaSmallAng
          Smallest angle $\approx 31.7^\circ$.

Q2. The same question in $\mathbb{R}^3$, and in $\mathbb{R}^d$, $d>3$.

Likely this question has been studied, in which case pointers to the literature would be appreciated.

Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • 10
    Yes, the vertices of an $n$-gon. Take the smallest inner angle of the convex hull and see how it is divided into $n-2$ angles by the rays from the corresponding vertex to all other points to show that $\pi/n$ or less is always there. – fedja Apr 05 '18 at 22:06
  • 1
    The problem can also be studied on the sphere, where circles through the north pole correspond to lines in the plane under stereographic projection, as that mapping is conformal, the intersection angles of circles on the sphere and between lines in the plane are the same. – Manfred Weis Apr 06 '18 at 10:55
  • Of course the stereographic projection equivalence generalizes to higher dimensions; the points on a regular n-gon, when centered at the origin, can be interpreted as the images of points on a sphere with its south pole at the origin, where the points have equal latitude and are evenly distributed. The analogue, when going to higher dimension n, would be an even distribution of the points in the intersection of an $n$-sphere with a hyperplane of dimension $n$, that is parallel to $\mathbb{R}^n$, i.e. on a $n-1$-sphere, thus supporting your assumption the projection is also an $n-1$ sphere. – Manfred Weis Apr 06 '18 at 18:38
  • @ManfredWeis: Thanks, but I don't see how to actually compute the optimal arrangement in 3D for arbitrary $n$, using the stereographic projection viewpoint. Perhaps it is like packing points on a sphere, with no clear theory except for special values of $n$. – Joseph O'Rourke Apr 06 '18 at 22:18

0 Answers0