Patterns in roots of integer-coefficient polynomials

Question

Below are shown two displays of all the roots of polynomials $$c_n x^n + c_{n-1} x^{n-1} + \cdots + c_1 x + c_0 \;=\; 0$$ with each coefficient $c_i$ an integer $|c_i| \le M$ (including $c_i=0$). No doubt this is all well-known, but I would be interested to learn what results explain the patterns in the distributions, especially the holes, both surrounding the real axis—in both shape and location—and the off-axis holes, perhaps more evident in the degree-$3$ plot than in the degree-$5$ plot.

---

         
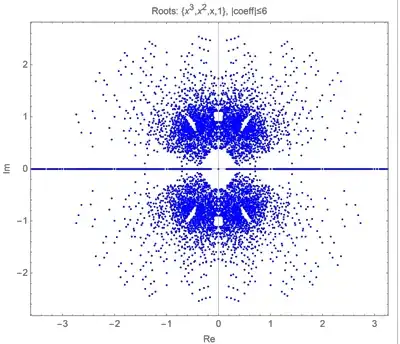
          ^{Roots of polynomials of degree $\le 3$ and integer coefficients $|c_i| \le 6$.}

---

         
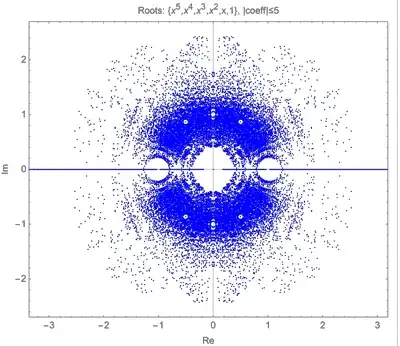
          ^{Roots of polynomials of degree $\le 5$ and integer coefficients $|c_i| \le 5$.}

---

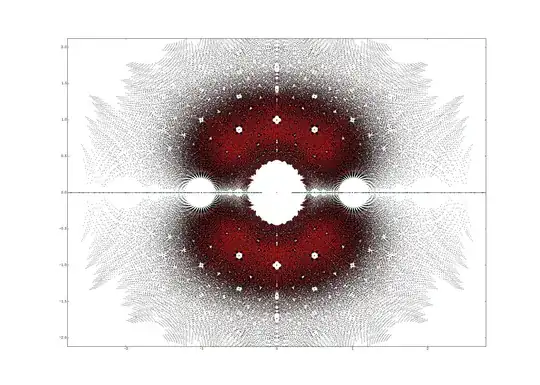
Addendum. User j.c. cited the article by John Baez on Dan Christensen's impressively detailed images, one of which I include below:

---

---

Answer 1

Suppose $P(z)$ is a polynomial with integer coefficients $|c_j| \le M$ and $z \ne 0$. If $c_k$ is the first nonzero coefficient, $$|P(z)|/|z|^k \ge |c_k| - \sum_{j=k+1}^d |c_j| |z|^j \ge 1 - \frac{M |z|}{1-|z|} >0 \ \ \text{if}\ \ |z| < \frac{1}{1+M}$$ This explains the hole around $z=0$. For the holes around $z=\pm 1$, first translate $z \to z\pm 1$.